Question

The magnitude of electric field outside the solenoid at a distance $r > R$ from its long central axis is

A. $\dfrac{{{\mu }_{0}}n{{I}_{\max }}\omega {{R}^{2}}}{2r}\sin \omega t$
B. $\dfrac{2{{\mu }_{0}}n{{I}_{\max }}\omega {{R}^{2}}}{r}\sin \omega t$
C. $\dfrac{{{\mu }_{0}}n{{I}_{\max }}\omega {{R}^{2}}}{3r}\sin \omega t$
D. $\dfrac{3{{\mu }_{0}}n{{I}_{\max }}\omega {{R}^{2}}}{2r}\sin \omega t$

Answer 1

Hint: From Gauss’s law we will get the expression for rate of change of magnetic flux. We also know that magnetic flux is given by the dot product of magnetic field and area. And the magnitude of the magnetic field inside a solenoid can be obtained by Ampere’s circuital law. Area is here is the area of a circle.

Formula used:
Gauss law,
$\int{E.dl=-\dfrac{d\phi }{dt}}$
Expression for magnetic flux,
${{\phi }_{B}}=B.A=\left| B \right|\left| A \right|\cos \theta $
Ampere’s circuital law,
$B={{\mu }_{0}}nI$

Complete step-by-step answer:
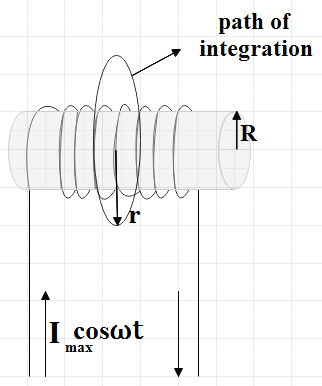
In the question we are given a solenoid of radius R with n number of turns. This solenoid is also carrying a time varying electric current given by,
$I={{I}_{\max }}\cos \omega t$ …………………. (1)
Where, ${{I}_{\max }}$ is the maximum current and ω is the angular frequency.
We are asked to find the electric field E at a distance $r > R$.
We know that the change in magnetic flux inside the solenoid induces an electric field. Let us represent this induced electric field by E.
At a distance $r > R$ we could apply Gauss’s law to get,
$\int{E.dl=-\dfrac{d\phi }{dt}}$ …………………… (2)
Where,$\dfrac{d\phi }{dt}$ = the change in magnetic flux.
But we know that, magnetic flux $\phi $through an area A in a uniform magnetic field B is the dot product of the magnetic field B and area A and it could be written as,
${{\phi }_{B}}=B.A=\left| B \right|\left| A \right|\cos \theta $ …………………. (3)
Where, θ is the angle between B and A.
Since, the magnetic field and the areal vector for the area under consideration is in the same direction, the angle between them is zero. That is,
$\Rightarrow \theta =0$
Equation (3) now becomes,
${{\phi }_{B}}=\left| B \right|\left| A \right|\cos 0=\left| B \right|\left| A \right|$ …………………….. (4)
We know that, the magnitude of magnetic field inside a solenoid of n number of turns per unit length and I current is given by Ampere’s circuital law as,
$B={{\mu }_{0}}nI$ …………………. (5)
Area under consideration is a circle, so,
$A=\pi {{r}^{2}}$ …………………….. (6)
Substituting (6) and (5) in (4), we get,
${{\phi }_{B}}=\left( {{\mu }_{0}}nI \right)\left( \pi {{r}^{2}} \right)$ ……………………. (7)
 Now we could substitute (7) in (2),
$\int{E.dl=-\dfrac{d\left( {{\mu }_{0}}nI \right)\left( \pi {{r}^{2}} \right)}{dt}}$
 Here, by integrating dl we get the circumference of the circular area under consideration because the small segment dl is a small part of the circle. Also ‘I’ is the only time varying quantity on the RHS. Therefore,
$\Rightarrow E\left( 2\pi r \right)=-{{\mu }_{0}}n\pi {{R}^{2}}\left( \dfrac{dI}{dt} \right)$
Substituting (1) we get,
$\Rightarrow E=\dfrac{-{{\mu }_{0}}n{{R}^{2}}}{2r}\left( \dfrac{d{{I}_{\max }}\cos \omega t}{dt} \right)$
$\Rightarrow E=\dfrac{{{\mu }_{0}}n{{I}_{\max }}\omega {{R}^{2}}}{2r}\sin \omega t$
Therefore, the magnitude of electric field outside the solenoid at a distance $r > R$ from its long central axis is $E=\dfrac{{{\mu }_{0}}n{{I}_{\max }}\omega {{R}^{2}}}{2r}\sin \omega t$.

So, the correct answer is “Option A”.

Note: Though both the methods of integration as well as differentiation are used here, the solving method is actually very simple. Since we already know that the area under consideration is a circle, we could simply get the line integral of the small element from the circumference of the circle. Also, the only time varying quantity in the RHS is current I, hence the differentiation part is also simple.