Question

The lengths of two sides of a triangle are 12 cm and 15 cm. between what two measures should the length of the third side will fall?

Answer 1

Hint: Use the concept given by “If a, b, and c are the three sides of any triangle then the length of third side ‘c’ ranges from (a – b) < c < (a + b)” and substitute the given values to get the range of third side of triangle. Then write the fall from higher value to lower value.


To solve the given question we will draw a triangle first so that we can solve the question with reference to the diagram therefore consider,


Complete step-by-step answer:

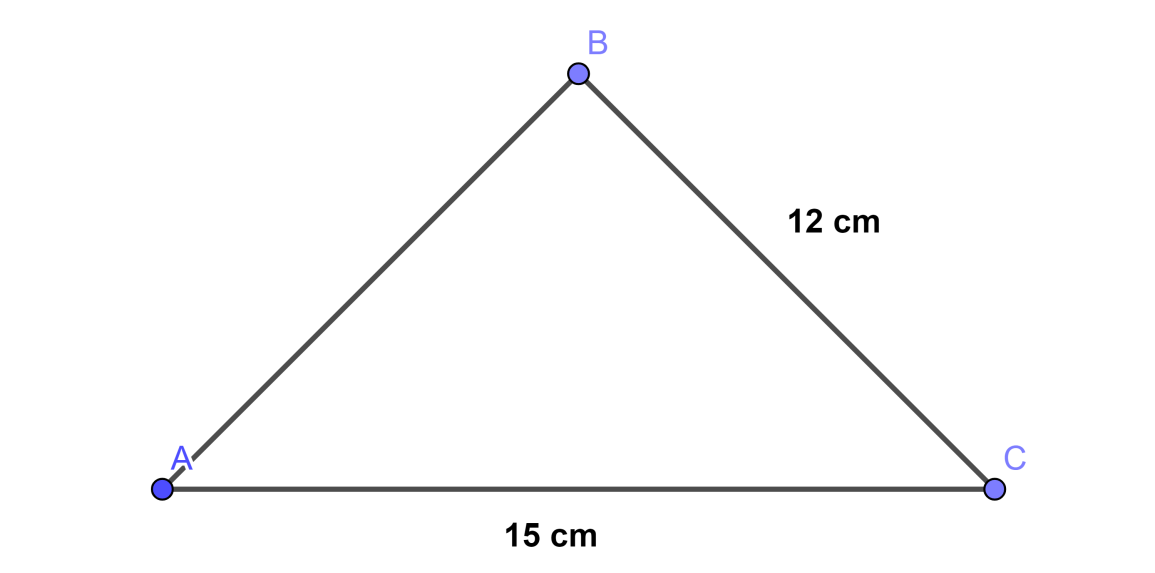
Now we will write the given data with assuming sides as in the diagram, therefore,

AC = 15 cm ………………………………………. (1)

BC = 12 cm ………………………………………. (2)

Now to find the fall of length AB which is the third side of the triangle ABC we should know the concept given below,

Concept:

If a, b, and c are the three sides of any triangle then the length of third side ‘c’ ranges from the value of subtraction of remaining two sides to the value of addition of remaining two sides, therefore,

(a – b) < c < (a + b)

As we have given the two sides AC and BC, therefore by using the above formula we can write the range of third side AB as follows, therefore,

(AC – BC) < AB < (AC + BC)

If we put the values of equation (1) and equation (2) in the above equation we will get,

Therefore, (15 – 12) < AB < (15 + 12)

By simplifying the above inequation we will get,

Therefore, 3 < AB < 27

As we have asked the fall of side AB therefore we have to write the answer from higher value to lower value, therefore we can say,

The fall of side AB is from 27 cm to 3 cm

Therefore if two sides of a triangle have lengths equal to 12 cm and 15 cm then the value of the third side will fall from 3 cm to 27 cm.

Note: Many students will subtract 15 from 12 and get a negative answer but do remember that the length is always positive therefore the negative answer gets rejected and ultimately you will get the positive answer.