Question

The length of the shadow of a tower on the plane ground is $\sqrt{3}$ times the tower. The angle of elevation of the sun is.
(a) ${{45}^{0}}$
(b) ${{30}^{0}}$
(c) ${{60}^{0}}$
(d) ${{90}^{0}}$

Answer 1

Hint:For solving this problem first we will draw the geometrical figure as per the given data. After that, we will use the basic formula of trigonometry $\tan \theta =\dfrac{\left( \text{length of the perpendicular} \right)}{\left( \text{length of the base} \right)}$ and $\tan {{30}^{0}}=\dfrac{1}{\sqrt{3}}$ . Then, we will solve correctly to get the elevation of the sun.

Complete step-by-step answer:
Given:
It is given that the length of the shadow of a tower on the plane ground is $\sqrt{3}$ times the tower and we have to find the elevation of the sun.
Now, first, we will draw a geometrical figure as per the given data. For more clarity look at the figure given below:

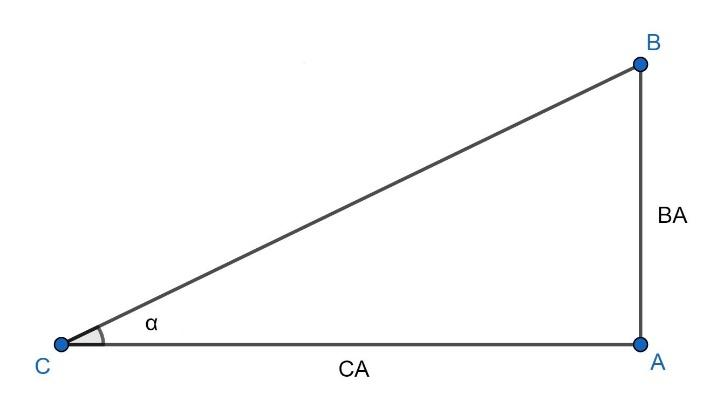
In the above figure BA represents the height of the tower, CA represents the length of the shadow of the tower and $\angle BCA=\alpha $ represents the elevation of the sun.
Now, as the tower stands vertical on the ground so, $\angle BAC={{90}^{0}}$ and it is given that the length of the shadow of a tower on the plane ground is $\sqrt{3}$ times the tower. Then,
$CA=\sqrt{3}\left( BA \right)...............\left( 1 \right)$
Now, consider $\Delta ABC$ in which $\angle BAC={{90}^{0}}$ , CA is equal to the length of the base, BA is equal to the length of the perpendicular and $\angle BCA=\alpha $. Then,
$\begin{align}
  & \tan \left( \angle BCA \right)=\dfrac{\left( \text{length of the perpendicular} \right)}{\left( \text{length of the base} \right)} \\
 & \Rightarrow \tan \alpha =\dfrac{BA}{CA} \\
\end{align}$
Now, substitute $CA=\sqrt{3}\left( BA \right)$ from the equation (1) in the above equation. Then,
$\begin{align}
  & \tan \alpha =\dfrac{BA}{CA} \\
 & \Rightarrow \tan \alpha =\dfrac{BA}{\sqrt{3}\left( BA \right)} \\
 & \Rightarrow \tan \alpha =\dfrac{1}{\sqrt{3}} \\
 & \Rightarrow \alpha ={{30}^{0}} \\
\end{align}$
Now, from the above result, we can say that the value of $\angle BCA=\alpha ={{30}^{0}}$ .
Thus, the angle of elevation of the sun will be ${{30}^{0}}$ .
Hence, (b) is the correct option.

Note: Here, the student should first try to understand what is asked in the problem. After that, we should try to draw the geometrical figure as per the given data. Students should remember the important trigonometric formulas, ratios and standard trigonometric angles for solving these types of problems.