Question

The length of the common chord of the circles \[{{x}^{2}}+{{y}^{2}}=12\text{ and }{{x}^{2}}+{{y}^{2}}-4x+3y-2=0\] is:
(a) \[4\sqrt{2}\]
(b) \[5\sqrt{2}\]
(c) \[2\sqrt{2}\]
(d) \[6\sqrt{2}\]

Answer 1

Hint: In this question, first of all, draw two circles and their common chord to visualize the question. Now, find the equation of the common chord by using \[{{S}_{1}}-{{S}_{2}}=0\]. Now, take a circle \[{{S}_{1}}:{{x}^{2}}+{{y}^{2}}-12=0\] and common chord and find the perpendicular distance from its center to chord by using \[\dfrac{\left| a{{x}_{1}}+b{{y}_{1}}+c \right|}{\sqrt{{{a}^{2}}+{{b}^{2}}}}\]. Now, use the Pythagoras theorem to find the value of the half part of the common chord and double it to get the required answer.

Complete step-by-step answer:
In this question, we have to find the length of the common chord of the circle \[{{x}^{2}}+{{y}^{2}}=12\text{ and }{{x}^{2}}+{{y}^{2}}-4x+3y-2=0\]. We have that standard equation of the circle in terms of its center and radius is of the form \[{{\left( x-{{x}_{1}} \right)}^{2}}+{{\left( y-{{y}_{1}} \right)}^{2}}={{r}^{2}}\] where \[\left( {{x}_{1}},{{y}_{1}} \right)\] is the center and r is the radius of the circle. Let us consider the circle given in the question.
\[{{x}^{2}}+{{y}^{2}}=12.....\left( i \right)\]
\[{{\left( x-0 \right)}^{2}}+{{\left( y-0 \right)}^{2}}={{\left( \sqrt{12} \right)}^{2}}\]
So, here center = (0, 0) and radius \[=\sqrt{12}\text{ }units......\left( ii \right)\]
\[{{x}^{2}}+{{y}^{2}}-4x+3y-2=0.....\left( iii \right)\]
By adding and substituting \[\left( 4+\dfrac{9}{4} \right)\] in the above equation, we get
\[{{x}^{2}}+{{y}^{2}}-4x+3x-2+\left( 4+\dfrac{9}{4} \right)-\left( 4+\dfrac{9}{4} \right)=0\]
\[\left( {{x}^{2}}-4x+4 \right)+\left( {{y}^{2}}+3x+\dfrac{9}{4} \right)+\left( -2 \right)-4-\dfrac{9}{4}=0\]
\[\left[ {{x}^{2}}-2.2x+{{\left( 2 \right)}^{2}} \right]+\left[ y+2.\dfrac{3}{2}x+{{\left( \dfrac{3}{2} \right)}^{2}} \right]=\dfrac{33}{4}\]
We know that \[{{a}^{2}}+{{b}^{2}}\pm 2ab={{\left( a\pm b \right)}^{2}}\]. By using this, we get,
\[{{\left( x-2 \right)}^{2}}+{{\left( y+\dfrac{3}{2} \right)}^{2}}={{\left( \sqrt{\dfrac{33}{2}} \right)}^{2}}\]
So, we get, the center \[\left( 2,\dfrac{-3}{2} \right)\text{ and radius as }\dfrac{\sqrt{33}}{2}....\left( iv \right)\]
Now, let us draw both the circles in the x – y plane.

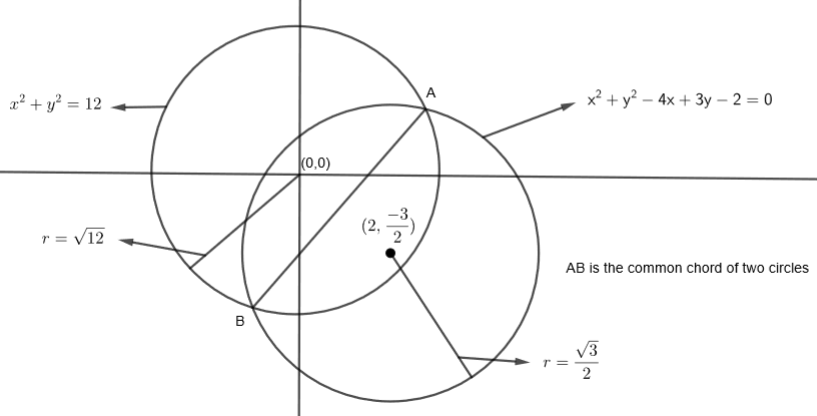
We know that the common chord of two circles \[{{S}_{1}}\text{ and }{{S}_{2}}\] is given by:
\[{{S}_{1}}-{{S}_{2}}=0\]
By substituting \[{{S}_{1}}\text{ and }{{S}_{2}}\] from equation (i) and (iii) respectively, we get,
Equation of common chord
\[\left( {{x}^{2}}+{{y}^{2}}-12 \right)-\left( {{x}^{2}}+{{y}^{2}}-4x+3y-2 \right)=0\]
\[-12+4x-3y+2=0\]
Equation of common chord = 4x – 3y – 10 = 0
Let us consider just the first circle and the chord.

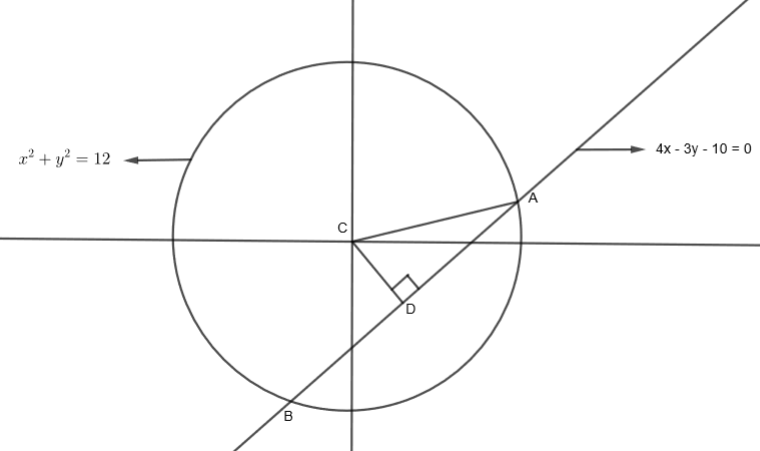
We know the perpendicular from the center of the circle divides the chord into two equal parts. So, let us find AB of the above figure. We know that from any point \[\left( {{x}_{1}},{{y}_{1}} \right)\], the length of the perpendicular on line ax + by + c = 0 is given by \[\dfrac{\left| a{{x}_{1}}+b{{y}_{1}}+c \right|}{\sqrt{{{a}^{2}}+{{b}^{2}}}}\]. So, from the point (0, 0), we get the length of the perpendicular on chord 4x – 3y – 10 as
\[CD=\left| \dfrac{4\left( 0 \right)-3\left( 0 \right)-10}{\sqrt{{{4}^{2}}+{{3}^{2}}}} \right|\]
\[CD=\left| \dfrac{-10}{\sqrt{16+9}} \right|\]
\[CD=\left| \dfrac{-10}{\sqrt{25}} \right|\]
\[CD=\left| \dfrac{-10}{5} \right|\]
\[CD=\left| -2 \right|\]
CD = 2 units
We know that in the above figure, AC that is the radius of the circle is equal to \[\sqrt{12}\text{ units}\].
So, by using the Pythagoras theorem in triangle ABC, we get,
\[{{\left( CD \right)}^{2}}+{{\left( AD \right)}^{2}}=A{{C}^{2}}\]
By substituting the value of AB = 2, \[AC=\sqrt{12}\], we get,
\[{{\left( 2 \right)}^{2}}+{{\left( AD \right)}^{2}}={{\left( \sqrt{12} \right)}^{2}}\]
\[4+{{\left( AD \right)}^{2}}=12\]
\[{{\left( AD \right)}^{2}}=12-4\]
\[{{\left( AD \right)}^{2}}=8\]
\[AD=\sqrt{8}=2\sqrt{2}\text{ units}\]
We know that length of the chord AB = 2 AD.
So, we get, \[AB=2\left( 2\sqrt{2} \right)\text{units}\].
\[AB=4\sqrt{2}\text{ units}\]
Hence, option (a) is correct.

Note: In this question, many students forget to double their answer and mark option (c) as answer which is wrong because we are asked to find the length of chord AB and not the half of it. Also, students can take any of the two circles to find the length of the common chord but it is advisable to take the the first circle that is \[{{x}^{2}}+{{y}^{2}}=12\] as it contains fewer variables and center is also (0, 0). So, there would be fewer calculations and hence less scope of mistakes.