Question

The length of a focal chord of the parabola \[{y^2} = 4ax\] at a distance b from the vertex is c, then:
A.\[2{a^2} = bc\]
B. \[{a^3} = {b^2}c\]
C. \[ac = {b^2}\]
D. \[{b^2}c = 4{a^3}\]

Answer 1

Hint: We draw a rough figure for the situation where we have a parabola and a focal chord of length c. Using the property of vertically opposite angles we have the angle made by the chord with x-axis equal on both sides of the axis. With the help or right triangle formed by the shortest distance from the vertex to the chord we find cosecant of the angle. Substitute the value of cosecant of the angle in the formula for length of a chord.
* Focal chord is a chord that passes through the focus of the parabola
* In a right triangle having angle\[\theta \], \[\sin \theta = \] perpendicularly divided by hypotenuse and \[\cos ec\theta = \dfrac{1}{{\sin \theta }}\].
*Length of focal chord of parabola \[{y^2} = 4ax\] making an angle \[\theta \] with the x-axis is given by \[4a\cos e{c^2}\theta \]

Complete step-by-step answer:

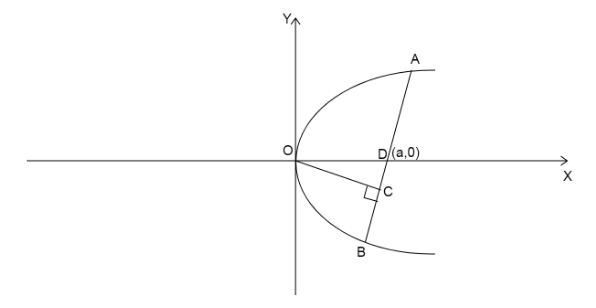
We are given a parabola \[{y^2} = 4ax\]
Let us assume that the chord cuts the X-axis at point D(a,0)
Then according to the question we are given the shortest distance from center to the chord is b.
Length of the focal chord is c.
The distance \[OD = a\].
Let us assume the focal chord makes an angle x with the X-axis.

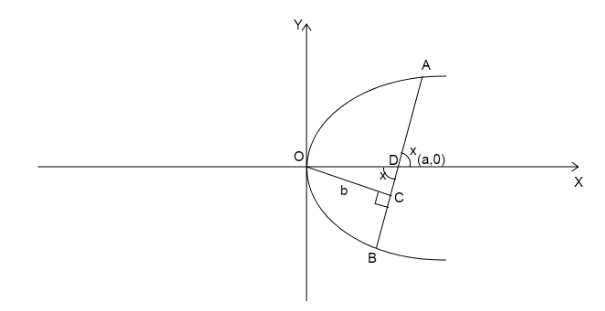
Since, we know vertically opposite angles are equal. Then, \[\angle ODC = x\].
Since, the shortest distance is the perpendicular distance, then \[\angle OCD = {90^ \circ }\].
In right triangle OCD,
\[\sin x = \dfrac{{OC}}{{OD}}\]
Substitute the value of OD as a and OC as b
\[ \Rightarrow \sin x = \dfrac{b}{a}\]
Since we know \[\cos ecx = \dfrac{1}{{\sin x}}\]
\[ \Rightarrow \cos ecx = \dfrac{1}{{\dfrac{b}{a}}}\]
\[ \Rightarrow \cos ecx = \dfrac{a}{b}\] … (1)
We know focal chord of a parabola \[{y^2} = 4ax\]making an angle \[\theta \]with the X-axis is of length \[4a\cos e{c^2}\theta \]
Therefore, we can write \[c = 4a\cos e{c^2}x\]
Substitute the value of \[\cos ecx\]from equation (1)
\[ \Rightarrow c = 4a{\left( {\dfrac{a}{b}} \right)^2}\]
Open the value on the bracket.
\[ \Rightarrow c = \dfrac{{4{a^3}}}{{{b^2}}}\]
Cross multiply the value in denominator of RHS to LHS
\[ \Rightarrow {b^2}c = 4{a^3}\]

Therefore, option D is correct.

Note: Students are likely to make the mistake of assuming the shortest distance as OD, which makes b equal to a. Keep in mind the shortest distance is the perpendicular distance and here the chord is not perpendicular to the x-axis so the perpendicular distance from vertex cannot be a.