Question

The image distance of an object placed \[10cm\] in front of a thin lens of focal length \[+5cm\]

Answer 1

Hint: The relation between object distance, image distance and focal length is given by the lens formula. Substituting corresponding values in the lens formula and putting the correct sign for each by following the sign convention will give us the required value of image distance.
Formulas Used:
\[\dfrac{1}{v}-\dfrac{1}{u}=\dfrac{1}{f}\]

Complete answer:
Refraction is the bending of rays of light when it passes from one medium to the other. When light passes through a lens, it undergoes refraction.

Given- focal length is \[+5cm\]. This means that it is a convex lens as convex lenses have positive focal lengths.
By convention all distances in front of the lens are taken as positive and distances behind the lens are taken as negative. Therefore, image distance in a convex lens is positive but object distance is negative.
The Lens formula is given by-
\[\dfrac{1}{v}-\dfrac{1}{u}=\dfrac{1}{f}\] - (1)
Here, \[v\] is the image distance from the centre of lens
\[u\] is the object distance from center of lens
\[f\] is focal length of the lens
Substituting the given values in eq (1), we have,
\[\begin{align}
  & \dfrac{1}{v}-\dfrac{1}{-10}=\dfrac{1}{5} \\
 & \dfrac{1}{v}=\dfrac{1}{5}-\dfrac{1}{10} \\
 & \Rightarrow \dfrac{1}{v}=\dfrac{1}{10} \\
\end{align}\]
 \[\therefore v=10cm\] - (2)
 The image distance is \[10cm\] in front of the lens, this is equal to object distance behind the lens. The image is formed at \[2f\], it is real, inverted and the same size as the object

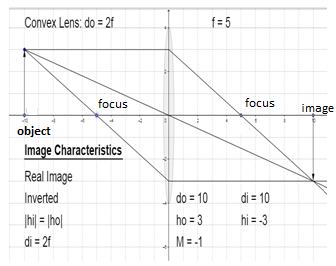
Here,
\[{{d}_{o}}\] is the object distance
\[{{d}_{i}}\] is the image distance
\[{{h}_{o}}\] is the object height
\[{{h}_{i}}\] is the image height
\[M\] is the magnification, that is, ratio of image height to object height

Note:
There are different image formations in a convex lens. It forms a virtual image if the object distance is \[u2f\] the image formed is diminished, real and inverted and formed beyond \[2f\].