Question

The height of a house subtends a right angle at the opposite window. The angle of elevation of the window from the base of the house is ${\text{60}^\circ }$. If the width of the road be 6 meters, find the height of the house
A) $6\sqrt 3 $
B) ${\text{3}}\sqrt {\text{6}} $
C) ${\text{5}}\sqrt {\text{3}} $
D) None of these

Answer 1

Hint: We can draw a diagram with the given details. We can divide the height of the building into two parts and find them separately using suitable trigonometric ratios. We can find the measure of unknown angles using angle sum property and complementary angles. We can add the 2 heights to get the total height of the house.

Complete step by step solution: We can draw a figure using the details given in the question.

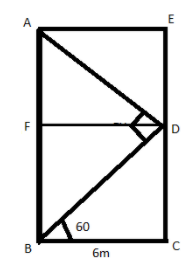
From the figure,
\[
  \angle DBC = 60^\circ \\
   \Rightarrow \angle FBD = \angle FBC - \angle DBC = 90^\circ - 60^\circ = 30^\circ \\
 \]
${\text{FD = BC = 6cm}}$
Consider right triangle BDF,
$
  {\text{tanB = }}\dfrac{{{\text{FD}}}}{{{\text{FB}}}} \\
   \Rightarrow {\text{tan3}}{{\text{0}}^{\text{o}}}{\text{ = }}\dfrac{{\text{6}}}{{{\text{FB}}}} \\
 $
Substituting the value of${\text{tan3}}{{\text{0}}^{\text{o}}}{\text{ = }}\dfrac{{\text{1}}}{{\sqrt {\text{3}} }}$, we get,
$
  \dfrac{1}{{\sqrt 3 }} = \dfrac{6}{{FB}} \\
   \Rightarrow FB = 6\sqrt 3 \\
 $
Consider right triangle ABD,
By angle sum property of triangle,
$\angle {\text{BAD + }}\angle {\text{ADB + }}\angle {\text{ABD = 180^\circ }}$
$
  \angle BAD = 180^\circ - \angle ADB - \angle ABD \\
   = 180^\circ - 90^\circ - 60^\circ = 30^\circ \\
 $
Now consider the right triangle ADF,
$
  {\text{tanA = }}\dfrac{{{\text{FD}}}}{{{\text{AF}}}} \\
   \Rightarrow {\text{tan6}}{{\text{0}}^{\text{o}}}{\text{ = }}\dfrac{{\text{6}}}{{{\text{AF}}}} \\
 $
Substituting the value of$\tan {60^{\text{o}}} = \sqrt 3 $, we get,
$
  \sqrt {\text{3}} {\text{ = }}\dfrac{{\text{6}}}{{{\text{AF}}}} \\
   \Rightarrow {\text{AF = }}\dfrac{{\text{6}}}{{\sqrt {\text{3}} }}{\text{ = 2}}\sqrt {\text{3}} \\
 $
Height of the house is given by,
$
  {\text{AB = AF + BF}} \\
  {\text{ = 6}}\sqrt {\text{3}} {\text{ + 2}}\sqrt {\text{3}} \\
  {\text{ = 8}}\sqrt {\text{3}} {\text{ m}} \\
 $
Therefore, height of the house is ${\text{8}}\sqrt {\text{3}} {\text{ m}}$.

So, the correct answer is option D.

Note: Drawing of the figure helps us a lot for understanding the question. We use complementary angles and angle sum property of the triangle to find the unknown angles. We must assume that the height of the house is perpendicular to the ground. We must write the units properly and must do the necessary conversions if needed. We must be familiar with the values of basic trigonometric functions.