Question

The graph of the equation \[ax+by+c=0\] may be of the form:
A.
B.

C.

D.

   

Answer 1

Hint:In the above question, we have been given the equation as \[ax+by+c=0\], which seems to be a linear equation in two variables and it happens to represent a straight line on the XY-plane on a graph.

Complete step-by-step answer:
The given equation \[ax+by+c=0\] is a linear equation in two variables which simply happens to represent a straight line.
So we will check the options given in the question one by one as follows to find out which form of the graph is of the equation \[ax+by+c=0\].
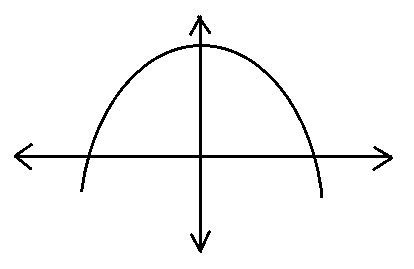
A.
  

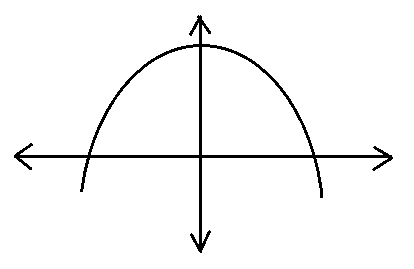
We know that \[ax+by+c=0\] is a straight line. Here, in the above curve, it is a downward parabola. It is not a straight line. So, this is not the correct form of the graph of the equation- \[ax+by+c=0\].
Hence, option A is not the correct answer of the question.
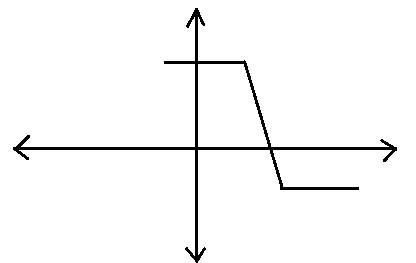
We will check for option B.
  

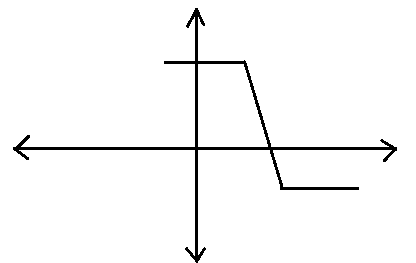
We know that \[ax+by+c=0\] is a straight line. Here, in the above figure, it is not a straight line. So, this is not the correct form of the graph of the equation- \[ax+by+c=0\].
Hence, optionB is not the correct answer to the question.
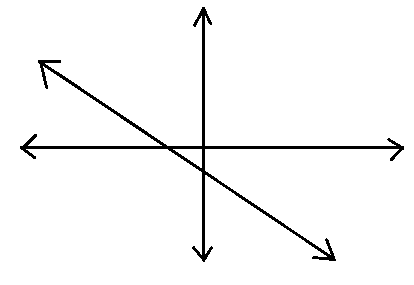
We will check for option C.

  

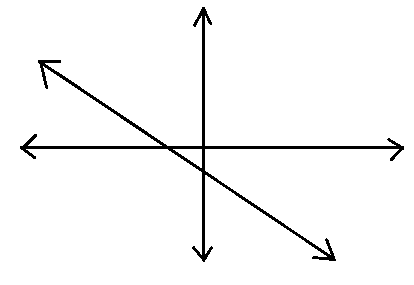
We know that \[ax+by+c=0\] is a straight line. Here, in the above figure, it is a straight line. So, this is the correct form of the graph of the equation- \[ax+by+c=0\].
Hence, option C is the correct answer of the question.
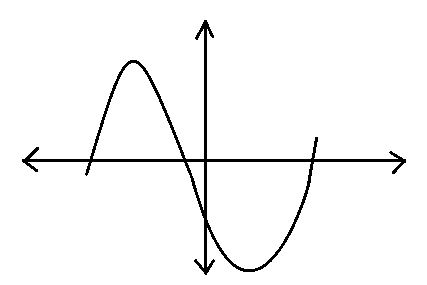
We also check for option D.
  

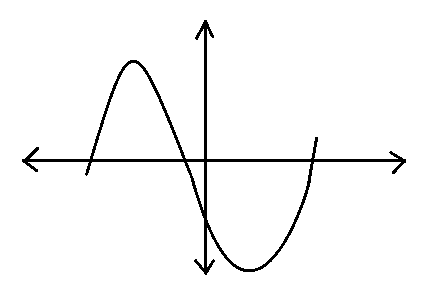
We know that \[ax+by+c=0\] is a straight line. Here, in the above figure, it is not a straight line. So, this is not the correct form of the graph of the equation- \[ax+by+c=0\].
Hence, option D is not the correct answer of the question.
Therefore, the correct option of the above question is C.

Note: Just remember the point that any linear equation in two variables represents a straight line.
Also, remember the condition on the linear equation in two variables \[ax+by+c=0\] that this equation will represent a straight line on the XY-plane if both a and b should not be zero, i.e. at least one of a and b is non-zero.