
Two men on either side of the cliff 90m height observe the angle of elevation of the top of the cliff to be 30 degrees and 60 degrees respectively. Find the distance between the two men.
Answer
583.8k+ views
Hint: First, draw a diagram of the given situation and assume the height of the cliff as ‘h’. Assume \[{{x}_{1}}\] and \[{{x}_{2}}\] as the distance of the first and second man respectively from the foot of the cliff. Then form two right-angle triangles and use \[\tan \theta =\dfrac{\text{perpendicular}}{\text{base}}\] to form expressions in terms of \[{{x}_{1}}\] and \[{{x}_{2}}\] where \['\theta '\] is the angle of the elevation. Then add \[{{x}_{1}}\] and \[{{x}_{2}}\] to get the answer.
Complete step-by-step solution:
First, let us draw a rough diagram of the given situation.
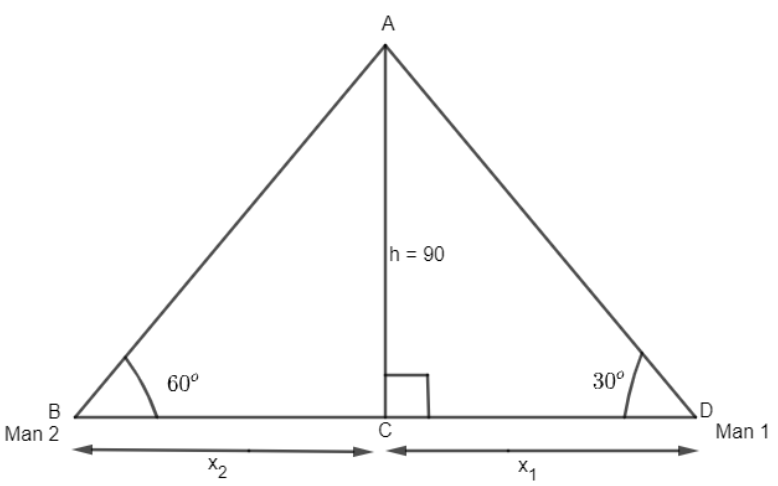
In the above figure, we have assumed AC as the cliff of the height is ‘h’. ‘A’ is the top of the cliff and ‘C’ is the foot of the cliff. Here, man 1 is assumed to be standing at point D at a distance of \[{{x}_{1}}\] from point C. And man 2 is assumed to be at point B at a distance of \[{{x}_{2}}\] from point C. The angle of elevation of the top of the cliff for man 1 and man 2 are 30 degrees and 60 degrees respectively.
Now, in right-angled triangle ACD, we have,
\[AC=h\]
\[CD={{x}_{1}}\]
\[\angle ADC={{30}^{\circ }}\]
Using \[\tan \theta =\dfrac{\text{perpendicular}}{\text{base}}\] where \['\theta '\] is the angle of elevation, we get,
\[\Rightarrow \tan {{30}^{\circ }}=\dfrac{AC}{CD}\]
\[\Rightarrow \tan {{30}^{\circ }}=\dfrac{h}{{{x}_{1}}}\]
\[\Rightarrow {{x}_{1}}=\dfrac{h}{\tan {{30}^{\circ }}}.....\left( i \right)\]
Now, in right angle triangle ACB, we have,
\[AC=h\]
\[CB={{x}_{2}}\]
\[\angle ABC={{60}^{\circ }}\]
Using \[\tan \theta =\dfrac{\text{perpendicular}}{\text{base}}\] we get,
\[\Rightarrow \tan {{60}^{\circ }}=\dfrac{AC}{CB}\]
\[\Rightarrow \tan {{60}^{\circ }}=\dfrac{h}{{{x}_{2}}}\]
\[\Rightarrow {{x}_{2}}=\dfrac{h}{\tan {{60}^{\circ }}}....\left( ii \right)\]
Now we can clearly see that the total distance between the two men is
\[BD=BC+CD\]
\[\Rightarrow BD={{x}_{1}}+{{x}_{2}}\]
So, adding equations (i) and (ii), we get,
\[\Rightarrow {{x}_{1}}+{{x}_{2}}=\dfrac{h}{\tan {{30}^{\circ }}}+\dfrac{h}{\tan {{60}^{\circ }}}\]
\[\Rightarrow {{x}_{1}}+{{x}_{2}}=h\left[ \dfrac{1}{\tan {{30}^{\circ }}}+\dfrac{1}{\tan {{60}^{\circ }}} \right]\]
Substituting \[h=90,\tan {{30}^{\circ }}=\dfrac{1}{\sqrt{3}},\tan {{60}^{\circ }}=\sqrt{3},\] we get,
\[\Rightarrow {{x}_{1}}+{{x}_{2}}=90\times \left[ \dfrac{1}{\dfrac{1}{\sqrt{3}}}+\dfrac{1}{\sqrt{3}} \right]\]
\[\Rightarrow {{x}_{1}}+{{x}_{2}}=90\times \left[ \sqrt{3}+\dfrac{1}{\sqrt{3}} \right]\]
\[\Rightarrow {{x}_{1}}+{{x}_{2}}=90\times \dfrac{4}{\sqrt{3}}\]
Rationalizing the denominator, we get,
\[\Rightarrow {{x}_{1}}+{{x}_{2}}=90\times \dfrac{4}{\sqrt{3}}\times \dfrac{\sqrt{3}}{\sqrt{3}}\]
\[\Rightarrow {{x}_{1}}+{{x}_{2}}=\dfrac{90\times 4\times \sqrt{3}}{3}\]
\[\Rightarrow {{x}_{1}}+{{x}_{2}}=120\sqrt{3}m\]
Substituting \[\sqrt{3}=1.732,\] we get,
\[\Rightarrow {{x}_{1}}+{{x}_{2}}=120\times 1.732\]
\[\Rightarrow {{x}_{1}}+{{x}_{2}}=207.84m\]
Hence, the distance between the two men is 207.84m.
Note: Students must remember that the side opposite to the assumed angle \['\theta '\] is always considered as perpendicular and that is why AC is considered as perpendicular in the two right-angle triangles. Now, we have used \[\tan \theta \] and not \[\sin \theta \] or \[\cos \theta \] in the right angle triangles. This is because we were provided the information regarding base and perpendicular but not the hypotenuse.
Complete step-by-step solution:
First, let us draw a rough diagram of the given situation.

In the above figure, we have assumed AC as the cliff of the height is ‘h’. ‘A’ is the top of the cliff and ‘C’ is the foot of the cliff. Here, man 1 is assumed to be standing at point D at a distance of \[{{x}_{1}}\] from point C. And man 2 is assumed to be at point B at a distance of \[{{x}_{2}}\] from point C. The angle of elevation of the top of the cliff for man 1 and man 2 are 30 degrees and 60 degrees respectively.
Now, in right-angled triangle ACD, we have,
\[AC=h\]
\[CD={{x}_{1}}\]
\[\angle ADC={{30}^{\circ }}\]
Using \[\tan \theta =\dfrac{\text{perpendicular}}{\text{base}}\] where \['\theta '\] is the angle of elevation, we get,
\[\Rightarrow \tan {{30}^{\circ }}=\dfrac{AC}{CD}\]
\[\Rightarrow \tan {{30}^{\circ }}=\dfrac{h}{{{x}_{1}}}\]
\[\Rightarrow {{x}_{1}}=\dfrac{h}{\tan {{30}^{\circ }}}.....\left( i \right)\]
Now, in right angle triangle ACB, we have,
\[AC=h\]
\[CB={{x}_{2}}\]
\[\angle ABC={{60}^{\circ }}\]
Using \[\tan \theta =\dfrac{\text{perpendicular}}{\text{base}}\] we get,
\[\Rightarrow \tan {{60}^{\circ }}=\dfrac{AC}{CB}\]
\[\Rightarrow \tan {{60}^{\circ }}=\dfrac{h}{{{x}_{2}}}\]
\[\Rightarrow {{x}_{2}}=\dfrac{h}{\tan {{60}^{\circ }}}....\left( ii \right)\]
Now we can clearly see that the total distance between the two men is
\[BD=BC+CD\]
\[\Rightarrow BD={{x}_{1}}+{{x}_{2}}\]
So, adding equations (i) and (ii), we get,
\[\Rightarrow {{x}_{1}}+{{x}_{2}}=\dfrac{h}{\tan {{30}^{\circ }}}+\dfrac{h}{\tan {{60}^{\circ }}}\]
\[\Rightarrow {{x}_{1}}+{{x}_{2}}=h\left[ \dfrac{1}{\tan {{30}^{\circ }}}+\dfrac{1}{\tan {{60}^{\circ }}} \right]\]
Substituting \[h=90,\tan {{30}^{\circ }}=\dfrac{1}{\sqrt{3}},\tan {{60}^{\circ }}=\sqrt{3},\] we get,
\[\Rightarrow {{x}_{1}}+{{x}_{2}}=90\times \left[ \dfrac{1}{\dfrac{1}{\sqrt{3}}}+\dfrac{1}{\sqrt{3}} \right]\]
\[\Rightarrow {{x}_{1}}+{{x}_{2}}=90\times \left[ \sqrt{3}+\dfrac{1}{\sqrt{3}} \right]\]
\[\Rightarrow {{x}_{1}}+{{x}_{2}}=90\times \dfrac{4}{\sqrt{3}}\]
Rationalizing the denominator, we get,
\[\Rightarrow {{x}_{1}}+{{x}_{2}}=90\times \dfrac{4}{\sqrt{3}}\times \dfrac{\sqrt{3}}{\sqrt{3}}\]
\[\Rightarrow {{x}_{1}}+{{x}_{2}}=\dfrac{90\times 4\times \sqrt{3}}{3}\]
\[\Rightarrow {{x}_{1}}+{{x}_{2}}=120\sqrt{3}m\]
Substituting \[\sqrt{3}=1.732,\] we get,
\[\Rightarrow {{x}_{1}}+{{x}_{2}}=120\times 1.732\]
\[\Rightarrow {{x}_{1}}+{{x}_{2}}=207.84m\]
Hence, the distance between the two men is 207.84m.
Note: Students must remember that the side opposite to the assumed angle \['\theta '\] is always considered as perpendicular and that is why AC is considered as perpendicular in the two right-angle triangles. Now, we have used \[\tan \theta \] and not \[\sin \theta \] or \[\cos \theta \] in the right angle triangles. This is because we were provided the information regarding base and perpendicular but not the hypotenuse.
Recently Updated Pages
Master Class 10 English: Engaging Questions & Answers for Success

Master Class 10 Social Science: Engaging Questions & Answers for Success

Master Class 10 Computer Science: Engaging Questions & Answers for Success

Class 10 Question and Answer - Your Ultimate Solutions Guide

Master Class 10 General Knowledge: Engaging Questions & Answers for Success

Master Class 10 Maths: Engaging Questions & Answers for Success

Trending doubts
A boat goes 24 km upstream and 28 km downstream in class 10 maths CBSE

State and explain Ohms law class 10 physics CBSE

Distinguish between soap and detergent class 10 chemistry CBSE

a Why did Mendel choose pea plants for his experiments class 10 biology CBSE

What is a "free hit" awarded for in limited-overs cricket?

Draw the diagram of the sectional view of the human class 10 biology CBSE




