Question

The graph of Kinetic Energy (K) of a body versus velocity (v) is represented as
(A) Hyperbola
(B) Parabola
(C) Straight line
(D) None of these

Answer 1

Hint
The kinetic energy of a body moving in a straight line is directly proportional to the square of its velocity. This also implies that it has a graph whose slope is not constant.
Formula used: $ K = \dfrac{1}{2}m{v^2} $ where $ m $ is the mass of the body and $ v $ is the velocity of its motion.

Complete step by step answer
Firstly, let us write down the formula for kinetic energy
 $\Rightarrow K = \dfrac{1}{2}m{v^2} $ where $ m $ is the mass of the body and $ v $ is the velocity of its motion.
For a graph of $ K $ versus $ v $, $ K $ is analogous to $ y $ and $ v $ is analogous to $ x $.
Thus, can be written representatively as $ y = a{x^2} $ where $ a $ is a constant equal to $ \dfrac{1}{2}m $.
Now, we compare each of the types of graph given in the option
First, the hyperbola:
The algebraic equation of a hyperbola centered at the origin is given as:
 $\Rightarrow \dfrac{{{x^2}}}{{{a^2}}} - \dfrac{{{y^2}}}{{{b^2}}} = 1 $ where $ a $ and $ b $ are constants.
Comparing this equation to $ y = a{x^2} $ it can be observed that no form of algebraic manipulation will make them the same since the variable $ y $ doesn’t have the same exponent. Thus, we can rule it out.
Next, we compare it to that of a parabola:
Equation of a parabola at the origin can be given as:
 $\Rightarrow y = 4p{x^2} $ where $ p $ is a constant
Comparing this to equation $ y = a{x^2} $, we can see that they are identical if we make $ a = 4p $. Thus, the equations are both equations of a parabola. In fact, $ y = 4p{x^2} $ is only called the focal point form while $ y = a{x^2} $ is called the Cartesian form.
The equation of a straight line is $ y = ax $. Comparing this with $ y = a{x^2} $ we also see that the exponent of $ x $ is not the same in the two equations. Thus, can be ruled out.
Therefore, we can conclude that the graph of kinetic energy versus velocity is represented by a parabola.
Hence, the correct option is B.

Note
Alternatively, we can actually compare the graphs each with a sketch of $ K $ against $ v $.
A quick sketch of $ K $ against $ v $ will give something similar to the graph below

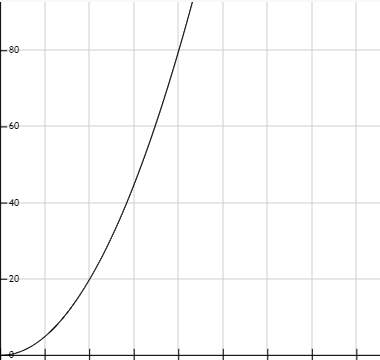
For hyperbola:

For parabola:

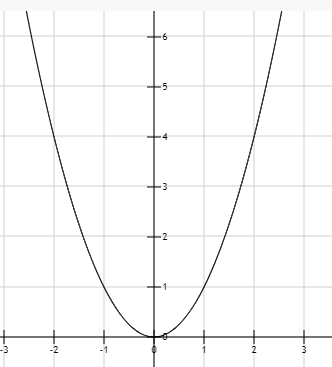
And for straight line:

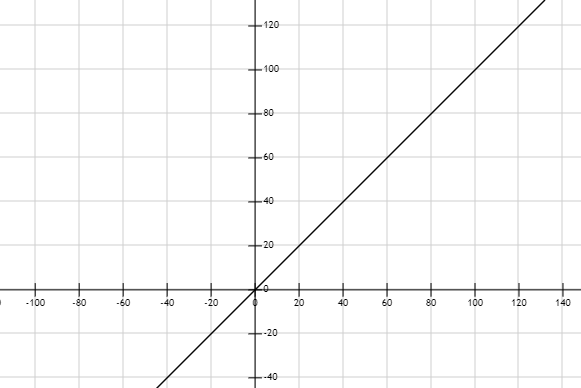
Comparing the graphs with the sketch of kinetic energy, we see that the most matching graph is that of the parabola but with the x-axis cut off.