Question

The foci of hyperbola \[9{{x}^{2}}-16{{y}^{2}}+18x+32y-151=0\] are
(a) (2, 3), (5, 7)
(b) (4, 1), (– 6, 1)
(c) (0, 0), (5, 2)
(d) None of these

Answer 1

Hint:First of all, convert the given equation into the standard hyperbolic equation of the form \[\dfrac{{{\left( x-h \right)}^{2}}}{{{a}^{2}}}-\dfrac{{{\left( y-k \right)}^{2}}}{{{b}^{2}}}=1\] and then write the focus of the hyperbola as \[\left( h\pm ae,k \right)\] where \[e=\sqrt{1+\dfrac{{{b}^{2}}}{{{a}^{2}}}}\]. Take care while converting the given equation into standard form.

Complete step-by-step answer:
In this question, we have to find the foci of the hyperbola \[9{{x}^{2}}-16{{y}^{2}}+18x+32y-151=0\]. First of all, let us convert the given equation into the standard hyperbolic equation. We know that the standard hyperbola is of the form \[\dfrac{{{\left( x-h \right)}^{2}}}{{{a}^{2}}}-\dfrac{{{\left( y-k \right)}^{2}}}{{{b}^{2}}}=1\] where h and k can be any constants. Let us now consider our equation.
\[9{{x}^{2}}-16{{y}^{2}}+18x+32y-151=0\]
By rearranging the terms of the above equation, we get,
\[\left( 9{{x}^{2}}+18x \right)-\left( 16{{y}^{2}}-32y \right)-151=0\]
We can also write this above equation as,
\[\left[ {{\left( 3x \right)}^{2}}+2\left( 3x \right)\left( 3 \right) \right]-\left[ {{\left( 4y \right)}^{2}}-2\left( 4y \right)\left( 4 \right) \right]-151=0\]
We know that by adding and subtracting the same constant equation remains the same. So, we get,
\[\left[ {{\left( 3x \right)}^{2}}+2\left( 3x \right)\left( 3 \right)+{{\left( 3 \right)}^{2}}-{{\left( 3 \right)}^{2}} \right]-\left[ {{\left( 4y \right)}^{2}}-2\left( 4y \right)\left( 4 \right)+{{\left( 4 \right)}^{2}}-{{\left( 4 \right)}^{2}} \right]-151=0\]
\[\left[ {{\left( 3x \right)}^{2}}+2\left( 3x \right)\left( 3 \right)+{{\left( 3 \right)}^{2}} \right]-{{\left( 3 \right)}^{2}}-\left[ {{\left( 4y \right)}^{2}}-2\left( 4y \right)\left( 4 \right)+{{\left( 4 \right)}^{2}} \right]+{{\left( 4 \right)}^{2}}-151=0\]
We know that \[{{a}^{2}}+{{b}^{2}}+2ab={{\left( a+b \right)}^{2}}\] and \[{{a}^{2}}+{{b}^{2}}-2ab={{\left( a-b \right)}^{2}}\]. By using these in the above equation, we get,
\[{{\left( 3x+3 \right)}^{2}}-9-{{\left( 4y-4 \right)}^{2}}+16-151=0\]
\[{{\left( 3x+3 \right)}^{2}}-{{\left( 4y-4 \right)}^{2}}-9+16-151=0\]
\[{{\left( 3x+3 \right)}^{2}}-{{\left( 4y-4 \right)}^{2}}-144=0\]
By taking out the common value from the above equation, we get,
\[9{{\left( x+1 \right)}^{2}}-16{{\left( y-1 \right)}^{2}}-144=0\]
By dividing 144 in the above equation, we get,
\[\dfrac{9{{\left( x+1 \right)}^{2}}}{144}-\dfrac{16{{\left( y-1 \right)}^{2}}}{144}=1\]
\[\dfrac{{{\left( x+1 \right)}^{2}}}{16}-\dfrac{{{\left( y-1 \right)}^{2}}}{9}=1\]
\[\dfrac{{{\left( x-\left( -1 \right) \right)}^{2}}}{{{\left( 4 \right)}^{2}}}-\dfrac{{{\left( y-1 \right)}^{2}}}{{{\left( 3 \right)}^{2}}}=1\]
By comparing the above equation by standard equation,
\[\dfrac{{{\left( x-h \right)}^{2}}}{{{a}^{2}}}-\dfrac{{{\left( y-k \right)}^{2}}}{{{b}^{2}}}=1\]
We get, h = – 1, k = 1, a = 4 and b= 3.
Let us first find the eccentricity (e) of this hyperbola, we know that
\[{{e}^{2}}=1+\dfrac{{{b}^{2}}}{{{a}^{2}}}\]
By substituting the value of a and b, we get,
\[{{e}^{2}}=1+\dfrac{{{3}^{2}}}{{{4}^{2}}}\]
\[{{e}^{2}}=\dfrac{{{4}^{2}}+{{3}^{2}}}{{{4}^{2}}}=\dfrac{16+9}{16}\]
\[{{e}^{2}}=\dfrac{25}{16}\]
Therefore, \[e=\sqrt{\dfrac{25}{16}}=\dfrac{5}{4}\]
Now, we know that the focus of the given hyperbola lies at \[\left( x,y \right)=\left( h\pm ae,k \right)\]
So, we get the first focus as
\[x=h+ae\]
\[x=-1+4\left( \dfrac{5}{4} \right)\]
\[x=4\]
\[y=k=1\]
So, (x, y) = (4, 1)
We get the second focus as,
\[x=h-ae\]
\[x=-1-4\left( \dfrac{5}{4} \right)\]
\[x=-6\]
\[y=k=1\]
So, (x, y) = (– 6, 1)
We can also draw the given hyperbola as

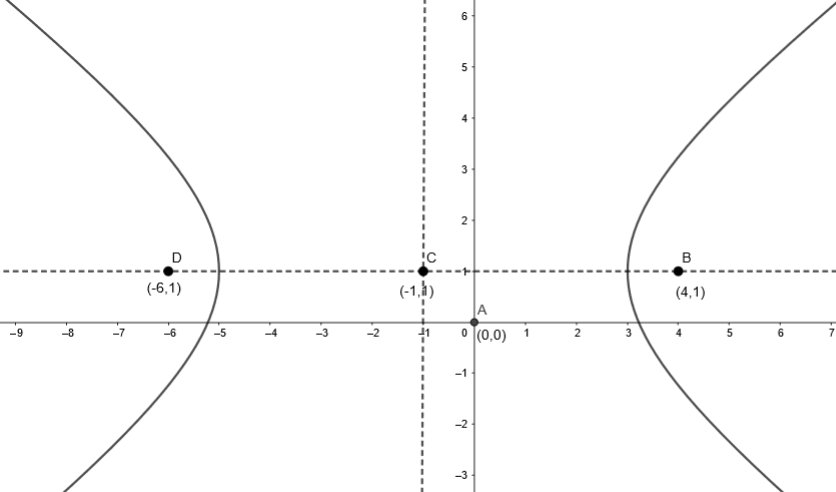
So, option (b) is the right answer.

Note: In this question, some students write the focus as \[\left( \pm ae,0 \right)\] which is wrong as that is true only for h = k = 0. But here, we can see that the vertex of the hyperbola is shifted. So, the focus would also shift accordingly. Also, students must take care that b is the conjugate axis while a is the transverse axis while finding the eccentricity. Also, for hyperbola, e is always greater than 1.