Question

The equation of the chord of contact of tangents drawn from the point \[\left( {2, - 3} \right)\] to the circle \[{x^2} + {y^2} + 4x - 6y - 12 = 0\] is
(A) \[4x - 6y - 17 = 0\]
(B) \[4x + 6y - 17 = 0\]
(C) \[4x + 6y + 17 = 0\]
(D) None of these

Answer 1

Hint: To find the equation of the chord of contact of tangents drawn from the point \[\left( {2, - 3} \right)\] to the circle, we will first put the given point in the equation of the given circle and find out whether it is greater than, less than or equal to zero. i.e., either the point lies outside, inside or on the circle. Then we will put the given point in the equation of the chord to find it.

Complete step-by-step solution:
The chord joining the points of contact of the two tangents to a conic drawn from a given point, outside it, is called the chord of contact of tangents.

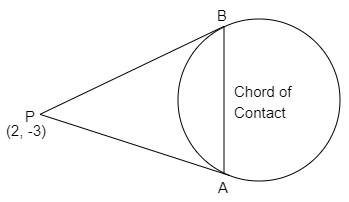
The equation of the chord of contact of tangents drawn from a point \[\left( {{x_1},{y_1}} \right)\] to the circle \[{x^2} + {y^2} + 2gx + 2fy + c = 0\] is given by \[{x_1}x + {y_1}y + g\left( {{x_1} + x} \right) + f\left( {{y_1} + y} \right) + c = 0\] . It is also written as \[T = 0\] .
Given circle is \[{x^2} + {y^2} + 4x - 6y - 12 = 0\]
Here, \[g = 2\] , \[f = - 3\] , \[c = - 12\]
Let \[P(2, - 3)\] be the point from where tangents are drawn.
Putting \[P(2, - 3)\] in the equation of given circle
\[ = {\left( 2 \right)^2} + {\left( { - 3} \right)^2} + 4\left( 2 \right) - 6\left( { - 3} \right) - 12\]
On solving,
\[ = 4 + 9 + 8 + 18 - 12\]
\[ = 27\] , which is greater than zero.
Hence, the point \[P(2, - 3)\] lies outside the circle.
Therefore, for point \[P(2, - 3)\] , equation of the chord of contact is given by
\[ \Rightarrow 2x - 3y + 2\left( {2 + x} \right) - 3\left( { - 3 + y} \right) - 12 = 0\]
On solving,
\[ \Rightarrow 2x - 3y + 4 + 2x + 9 - 3y - 12 = 0\]
\[ \Rightarrow 4x - 6y + 1 = 0\]
Therefore, the equation of the chord of contact of tangents drawn from the point \[\left( {2, - 3} \right)\] to the circle is \[4x - 6y + 1 = 0\] .
Hence, option (D) is correct.

Note: The equation of the tangent on a point of the circle and the equation of a chord of contact are both given by \[T = 0\] . The difference is that in the case of a chord of contact point \[P\] lies outside the circle while in the case of a tangent the point \[P\] lies on the circle.