Question

The e.m.f. of the cell shown in the figure is

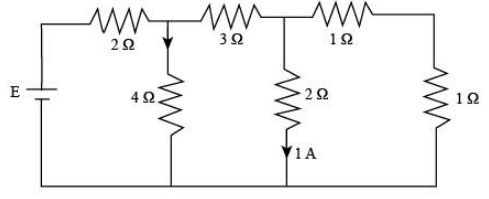
(A) $12\;{\rm{V}}$
(B) $13\;{\rm{V}}$
(C) $16\;{\rm{V}}$
(D) $18\;{\rm{V}}$

Answer 1

Hint:First, we will draw the circuit diagram with current distribution in various resistance and resolve some resistance to get some idea about current flow. After this, we can apply KVL in the various loops of the circuit to determine the emf of the cell.

Complete step by step answer:
Draw the circuit diagram with the current distribution.

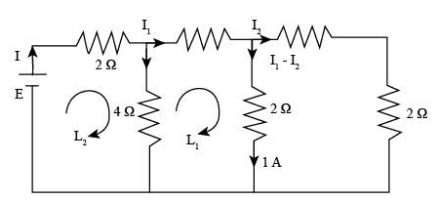
In the diagram, we resolve the two right-side resistance, which is in series. Here, we will calculate the voltage across A and B, so
$
{V_A} - {V_B} = 2\;\Omega \times 1\;{\rm{A}}\\
\Rightarrow{V_A} - {V_B} = 2\;{\rm{V}}
$
Now we know that the ${V_A} - {V_B} = 2\;{\rm{V}}$, so calculate current ${I_2}$ with the help of ${V_A} - {V_B}$.
Therefore, we get
$
2\;{\rm{V}} = {I_2} \times 2\;\Omega \\
\Rightarrow{I_2} = \dfrac{{2\;{\rm{V}}}}{{2\;\Omega }}\\
\Rightarrow{I_2} = 1\;{\rm{A}}$
From the diagram we will use ${I_1} - {I_2} = \;{\rm{1A}}$ for the determination of ${I_1}$ current, so substitute the value of \[{I_2}\] equation.
\[
{I_1} - 1\;{\rm{A}} = 1\;{\rm{A}}\\
\Rightarrow {I_1} = 2\;{\rm{A}}
\]
Now, we will apply the KVL in loop ${L_1}$ to determine the current $I$.
Therefore, we get
$\left( { - 2\;\Omega {I_1}} \right) - \left( {2\;\Omega
\times 1\;{\rm{A}}} \right) + 6\;\Omega \left( {I - {I_1}} \right) = 0$
Here, we use a negative sign where the current direction is clockwise and a positive sign where the current direction is anticlockwise in the circuit.
Substitute ${I_1} = 2\;{\rm{A}}$ in the above equation.
\[
\left( { - 2\;\;\Omega \times 2\;{\rm{A}}} \right) - \left( {2\;\Omega \times 1\;{\rm{A}}} \Rightarrow\right) + 6\;\Omega \left( {I - 2\;{\rm{A}}} \right) = 0\\
\Rightarrow \left( { - 4\;{\rm{V}}} \right) - \left( {2\;{\rm{V}}} \right) + 6\;\Omega I - 12\;{\rm{V}} = 0\\
\Rightarrow I = \dfrac{{18\;{\rm{V}}}}{{6\;\Omega }}\\
\Rightarrow I = 3\;{\rm{A}}
\]
Again we will apply KVL in the loop ${L_2}$ to determine the emf of the cell.
Therefore, we get
$E - 2\;\Omega I - 6\;\Omega \left( {I - {I_1}} \right) = 0$
Here, $E$ is the e.m.f of the cell.
Substitute the values in the above equation.
\[
E - 2\;\Omega \left( {{\rm{3}}\;{\rm{A}}} \right) - 6\;\Omega \left( {{\rm{3}}\,{\rm{A - 2}}\;{\rm{A}}} \right) = 0\\
\Rightarrow E - 6\;{\rm{V}} - 6\;{\rm{V}} = 0\\
\therefore E = 12\;V\]

Therefore, e.m.f. of the cell is $12\;{\rm{V}}$ and option (A) is correct.

Note:In this question, the application of KVL is an important part of the solution. So, use the correct sign convention while applying the KVL in the two loops of the circuits. If we use the wrong sign convention, then our calculation will become wrong, and we will get the incorrect value of the e.m.f of the cell.