Question

The diameter of a garden roller is \[1.4\] m and 2 m long. How much area will it cover in 5 revolutions?

Answer 1

Hint:
First, we will find the radius of the roller from the given diameter. Then we will use the formula of the curved surface area of circle \[2\pi rh\] and then multiply it by \[n\] to find the area covered in \[n\] revolutions.

Complete step by step solution:
Given that the diameter of the roller \[d\] is \[1.4\] and the length of the roller \[h\] is 2 m.

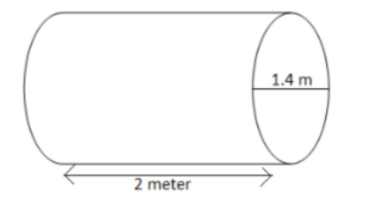
We will find the radius \[r\] from the diameter of the roller.
\[
   \Rightarrow r = \dfrac{{1.4}}{2} \\
   \Rightarrow r = 0.7{\text{ m}} \\
 \]
We know that if the roller completes one revolution, then the area covered is the curved surface area of a garden roller \[2\pi rh\].
Now we will find the area covered in 5 revolutions using the formula of the curved surface area of a garden roller.
\[{\text{Area covered in 5 revolutions = }}5 \times 2\pi rh\]
Substituting the values of \[r\] and \[h\] in the above equation, we get
\[
   \Rightarrow 5 \times 2 \times \dfrac{{22}}{7} \times 0.7 \times 2 \\
   \Rightarrow 10 \times 22 \times 0.1 \times 2 \\
   \Rightarrow 44{\text{ }}{{\text{m}}^2} \\
 \]

Thus, the area covered in 5 revolutions is 44 m\[^2\].

Note:
Note: In these types of questions, we should make a diagram to understand the given question properly. In general the total surface area of the cylinder is \[2\pi rh + 2\pi {r^2}\], where \[r\] is radius and \[h\] is height, but in this question we only need to consider curved surface area, \[2\pi rh\]. So we need to take care of calculating the area of one revolution.