Question

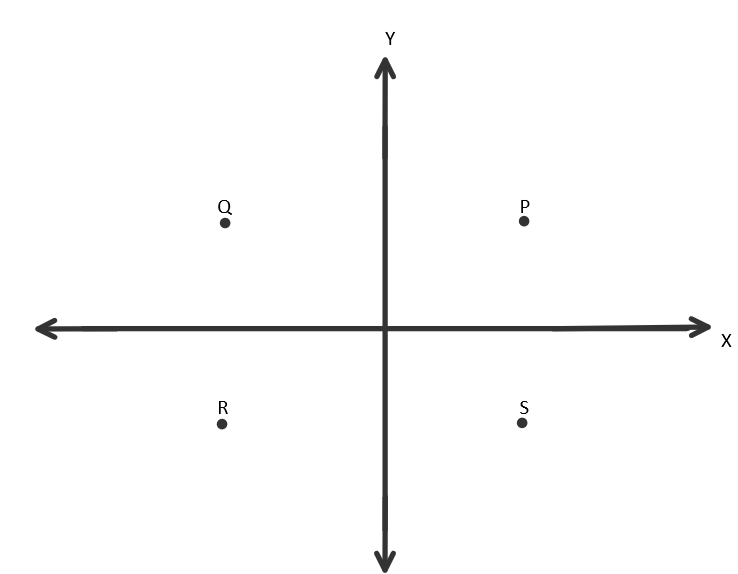
The diagram shows the four quadrants P, Q, R and S on a Cartesian plane. Which of the following points lie in the quadrant S?
\[\begin{align}
  & \text{I (-1,2) II (-1,-2)} \\
 & \text{III (1,-2) IV (2,-1) } \\
\end{align}\]

\[\begin{align}
  & \text{(A) I and II only} \\
 & \text{(B) I and IV only} \\
 & \text{(C) II and III only} \\
 & \text{(D) III and IV only} \\
\end{align}\]

Answer 1

Hint: From the given point, we have to find whether the abscissa and ordinate is greater than zero (or) less than zero. Once the sign of the abscissa and ordinate is determined, we can say in which quadrant the given point lies on the coordinate system.

Complete step-by-step solution -
Before solving the question, we should have an idea of the concept of quadrants.
Let us assume a point \[\text{A(}{{\text{x}}_{1}},{{\text{y}}_{1}})\]in the coordinate system.

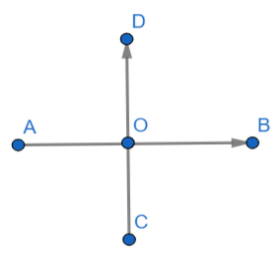
A point \[\text{A(}{{\text{x}}_{1}},{{\text{y}}_{1}})\]is said to be in \[{{1}^{st}}\] quadrant if the point lies in the region DOB.
A point \[\text{A(}{{\text{x}}_{1}},{{\text{y}}_{1}})\]is said to be in \[{{2}^{nd}}\] quadrant if the point lies in the region DOA.
A point \[\text{A(}{{\text{x}}_{1}},{{\text{y}}_{1}})\]is said to be in \[{{3}^{rd}}\] quadrant if the point lies in the region COA.
A point \[\text{A(}{{\text{x}}_{1}},{{\text{y}}_{1}})\]is said to be in \[{{4}^{th}}\] quadrant if the point lies in the region COB.
A point \[\text{A(}{{\text{x}}_{1}},{{\text{y}}_{1}})\]is said to be \[{{1}^{st}}\] quadrant if \[{{x}_{1}}>0,{{\text{y}}_{1}}>0\].
A point \[\text{A(}{{\text{x}}_{1}},{{\text{y}}_{1}})\]is said to be \[{{2}^{nd}}\] quadrant if \[{{x}_{1}}<0,{{\text{y}}_{1}}>0\].
A point \[\text{A(}{{\text{x}}_{1}},{{\text{y}}_{1}})\]is said to be \[{{3}^{rd}}\] quadrant if \[{{x}_{1}}<0,{{\text{y}}_{1}}<0\].
A point \[\text{A(}{{\text{x}}_{1}},{{\text{y}}_{1}})\]is said to be \[{{4}^{th}}\] quadrant if \[{{x}_{1}}>0,{{\text{y}}_{1}}<0\].

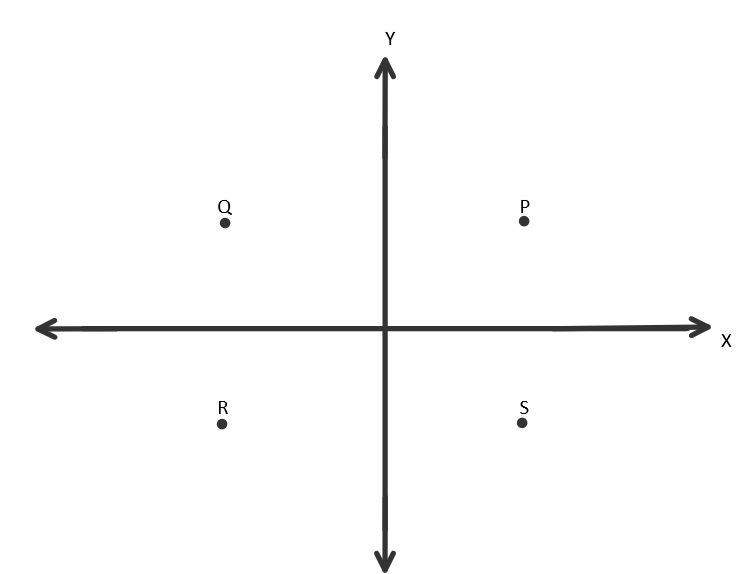
From the above diagram, it is clear that
Region P represents \[{{1}^{st}}\] quadrant.
Region Q represents \[{{2}^{nd}}\] quadrant.
Region R represents \[{{3}^{rd}}\] quadrant.
Region S represents \[{{4}^{th}}\]quadrant.
We have given four points in the question.
\[\begin{align}
  & \text{I (-1,2) II (-1,-2)} \\
 & \text{III (1,-2) IV (2,-1) } \\
\end{align}\]
We have to compare each and every point with \[\text{A(}{{\text{x}}_{1}},{{\text{y}}_{1}})\].
From \[\text{I (-1},2)\], we can say that \[{{x}_{1}}=-1,{{y}_{1}}=2\] .In this point, \[{{x}_{1}}<0,{{\text{y}}_{1}}>0\]. Hence, \[\text{I (-1},2)\] is said to be in \[{{2}^{nd}}\] quadrant.
From \[\text{II (-1},-2)\], we can say that \[{{x}_{1}}=-1,{{y}_{1}}=-2\].In this point, \[{{x}_{1}}<0,{{\text{y}}_{1}}<0\]. Hence,\[\text{II (-1},-2)\] is said to be in \[{{3}^{rd}}\] quadrant.
From \[\text{III (1},-2)\], we can say that \[{{x}_{1}}=1,{{y}_{1}}=-2\] .In this point, \[{{x}_{1}}>0,{{\text{y}}_{1}}<0\]. Hence,\[\text{III (1},-2)\] is said to be in \[{{4}^{th}}\] quadrant.
From \[\text{IV (2},-1)\], we can say that \[{{x}_{1}}=2,{{y}_{1}}=-1\] .In this point, \[{{x}_{1}}>0,{{\text{y}}_{1}}>0\]. Hence,\[\text{IV (2},-1)\] is said to be in\[{{4}^{th}}\] quadrant.
So, we can say that \[\text{III (1},-2)\] and \[\text{IV (2},-1)\] are in the region S.
Hence points \[\text{III}\] and \[\text{IV}\]are the point lie in the region S.
Hence, option (D) is correct.

Note: Remember that if the abscissa of a point is equal to zero, then the point is said to lie on the y-axis but not in any of the four quadrants. If the ordinate of a point is equal to zero, then the point is said to lie on the x-axis but not in any of the four quadrants. So, a point is said to be any of the four quadrants if and only if the abscissa and ordinate should not be equal to zero.