Question

The d electron configuration of $C{r}^{2+}$,$M{n}^{2+}$,$F{e}^{2+}$and $N{i}^{2+}$ are $3d^4$,$3d^5$,$3d^6$and $3d^8$ respectively. Which one of the following aqua complexes will exhibit the minimum paramagnetic behaviour ? (At. No. Cr = 24, Mn = 25, Fe = 26, Ni = 28)
a.) $[Cr(H_{2}O{)}_6{]}^{2+}$
b.) $[Mn(H_{2}O{)}_6{]}^{2+}$
c.) $[Fe(H_{2}O{)}_6{]}^{2+}$
d.) $[Ni(H_{2}O{)}_6{]}^{2+}$

Answer 1

Hint: The paramagnetic species have unpaired electrons. Higher the number of unpaired electrons, more will be the magnetic moment or paramagnetic character, This can be calculated as -
$\mu =\sqrt{n(n+1)}$
Where n = number of unpaired electrons

Complete step by step answer :
First, let us understand what is paramagnetic behaviour and what are the conditions that are required to achieve it.
The paramagnetic are those species that have unpaired electrons. The first condition for a species to be paramagnetic is that it must have at least one free electron. When the magnet is placed near a paramagnetic species, the free electrons in the mass get aligned up in the direction of the magnet.
The paramagnetic behaviour in a species leads to the formation of the net magnetic moment. The magnetic moment can be calculated by the formula -
$\mu =\sqrt{n(n+1)}$
Where n = number of unpaired electrons
The water has charge 0 on it. So, all these metals are in +2 oxidation states.
So, let us see the electrons in 3d orbitals of these transition metals according to their electronic configurations which are given to us and calculate their magnetic moment.
So, the first species is Chromium with +2 charge. It has 4 electrons in 3d orbital. So, the filling will take place as-

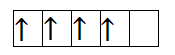
So, from the above filling, it is clear that there are four unpaired electrons. Thus, the magnetic moment is-
$\mu =\sqrt{n(n+1)}$
$\mu =\sqrt{4(4+1)}$
$\mu =\sqrt{4\times 5}$
$\mu =\sqrt{20}$
µ = 4.47 BM
Now, let us calculate for $M{n}^{2+}$. It has 4 electrons in 3d orbital. So, the filling will take place as-

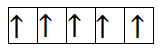
From the above filling, it is clear that there are five unpaired electrons. Thus, the magnetic moment is-
$\mu =\sqrt{n(n+1)}$
$\mu =\sqrt{5(5+1)}$
$$\mu =\sqrt{5\times 6}$$
$\mu =\sqrt{30}$
µ = 5.47 BM
Now, let us calculate for $F{e}^{2+}$. It has 6 electrons in 3d orbital. So, the filling will take place as-

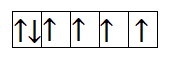
From the above filling, it is clear that there are four unpaired electrons. Thus, the magnetic moment is-
$\mu =\sqrt{n(n+1)}$
$\mu =\sqrt{4(4+1)}$
$\mu =\sqrt{4\times 5}$
$\mu =\sqrt{20}$
µ = 4.47 BM
Now, let us calculate for $N{i}^{2+}$. It has 8 electrons in 3d orbital. So, the filling will take place as-

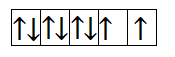
From the above filling, it is clear that there are two unpaired electrons. Thus, the magnetic moment is-
$\mu =\sqrt{n(n+1)}$
$\mu =\sqrt{2(2+1)}$
$\mu =\sqrt{2\times 3}$
$\mu =\sqrt{6}$
µ = 2.44 BM
So, observing all the values, we can say that $[Ni(H_{2}O{)}_6{]}^{2+}$ with eight electrons in 3d orbital has least paramagnetic character,

So, the option (d) is the correct answer.

Note: It must be noted that n is the number of unpaired electrons and not the total number of electrons in d orbital. Further, the water is a neutral ligand. It does not have any positive or negative charge. So, the total charge on a complex like here is +2 will be taken as the charge on the metal ion.