
The cost of 2 kg of apples and 1 kg grapes on a day was bound to be Rs. 160. After a month the cost of 4 kg apples and 2 kg grapes is Rs. 300. Represent this situation algebraically and geometrically.
Answer
511.2k+ views
Hint: We start solving the problem by assigning the variables for the cost of one apple and one grape. We then write the equation for the given condition that the cost of 2 kg of apples and 1 kg grapes on a day was bound to be Rs. 160. We the write the equation for the cost of 4 kg apples and 2 kg grapes is Rs. 300. We then find the points that lie on two of the obtained equations. We then plot the obtained equations to get the required result.
Complete step by step answer:
According to the problem, we are given that the cost of 2 kg of apples and 1 kg grapes on a day was bound to be Rs. 160. After a month the cost of 4 kg apples and 2 kg grapes is Rs. 300. We need to represent this given situation algebraically and geometrically.
Let us assume the cost of the one kg of apple be ‘x’ and the cost of one kg of grape be ‘y’.
We have given that the cost of 2 kg of apples and 1 kg grapes on a day was bound to be Rs. 160.
So, we get $2x+y=160$ ---(1).
We are also given that the cost of 4 kg apples and 2 kg grapes is Rs. 300.
So, we get $4x+2y=300$ ---(2).
We need to solve the system of linear equations shown below to find the cost of apples and cost of grapes.
$2x+y=160$ ---(3).
$4x+2y=300$ ---(4).
Let us find the points that lies on equation (3).
So, we have $y=160-2x$.
Let us find the points that lies on equation (4).
So, we have $y=\dfrac{300-4x}{2}$.
$\Rightarrow y=150-2x$
Let us plot the system of linear equations using the obtained values of x and y-coordinates.
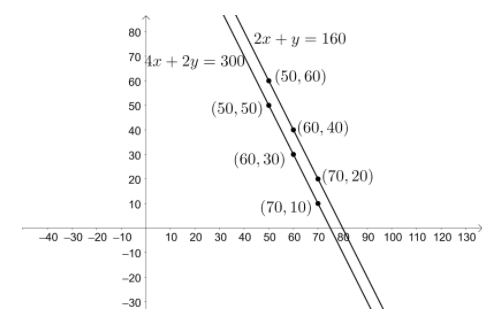
We can see that the two linear equations represent parallel lines which tells us that there is no feasible solution.
Note: Here we assumed that the cost of one kg apples and cost of one kg grapes does not change after the end of month. Whenever we get this type of problem, we start solving the problem by assuming the variables for the unknowns present in the problem. We should know that the feasible solution will be obtained if the feasible region of both the equations coincide. Similarly, we can expect problems to find the perpendicular distance between the parallel lines obtained.
Complete step by step answer:
According to the problem, we are given that the cost of 2 kg of apples and 1 kg grapes on a day was bound to be Rs. 160. After a month the cost of 4 kg apples and 2 kg grapes is Rs. 300. We need to represent this given situation algebraically and geometrically.
Let us assume the cost of the one kg of apple be ‘x’ and the cost of one kg of grape be ‘y’.
We have given that the cost of 2 kg of apples and 1 kg grapes on a day was bound to be Rs. 160.
So, we get $2x+y=160$ ---(1).
We are also given that the cost of 4 kg apples and 2 kg grapes is Rs. 300.
So, we get $4x+2y=300$ ---(2).
We need to solve the system of linear equations shown below to find the cost of apples and cost of grapes.
$2x+y=160$ ---(3).
$4x+2y=300$ ---(4).
Let us find the points that lies on equation (3).
So, we have $y=160-2x$.
| x | 60 | 50 | 70 |
| y | 40 | 60 | 20 |
Let us find the points that lies on equation (4).
So, we have $y=\dfrac{300-4x}{2}$.
$\Rightarrow y=150-2x$
| x | 60 | 50 | 70 |
| y | 30 | 50 | 10 |
Let us plot the system of linear equations using the obtained values of x and y-coordinates.

We can see that the two linear equations represent parallel lines which tells us that there is no feasible solution.
Note: Here we assumed that the cost of one kg apples and cost of one kg grapes does not change after the end of month. Whenever we get this type of problem, we start solving the problem by assuming the variables for the unknowns present in the problem. We should know that the feasible solution will be obtained if the feasible region of both the equations coincide. Similarly, we can expect problems to find the perpendicular distance between the parallel lines obtained.
Recently Updated Pages
Master Class 9 Social Science: Engaging Questions & Answers for Success

Master Class 9 Science: Engaging Questions & Answers for Success

Master Class 9 English: Engaging Questions & Answers for Success

Master Class 9 Maths: Engaging Questions & Answers for Success

Master Class 11 Economics: Engaging Questions & Answers for Success

Master Class 11 English: Engaging Questions & Answers for Success

Trending doubts
Which places in India experience sunrise first and class 9 social science CBSE

Fill the blanks with the suitable prepositions 1 The class 9 english CBSE

Write the 6 fundamental rights of India and explain in detail

Difference Between Plant Cell and Animal Cell

What is the Full Form of ISI and RAW

Golden Revolution is related to AFood production BOil class 9 social science CBSE




