Question

The common tangents to the circle ${x^2} + {y^2} = 2$ and the parabola ${y^2} = 8x$ touch the circle at the points P, Q, and the parabola at the points R, S. Then the area of the quadrilateral PQRS is
A) 3
B) 6
C) 9
D) 15

Answer 1

Hint: Tangents are the straight lines that touch the curve at one point only. That point is called the point of contact.
 The slope of the tangents to any curve $y = f\left( x \right)$ is given by the derivative $\dfrac{{dy}}{{dx}}$ .
The common tangents to a given circle and parabola must have an equal slope.
Find the slopes of tangents of circle and parabola and equate them to find the points of contact.
The circle and parabola both are symmetric figures, resulting in two common tangents.
 Finding points of contact of one tangent line will correspondingly give the points of contact of other tangent lines as well.

Complete step-by-step answer:
Step 1: Find the slope of the common tangent:

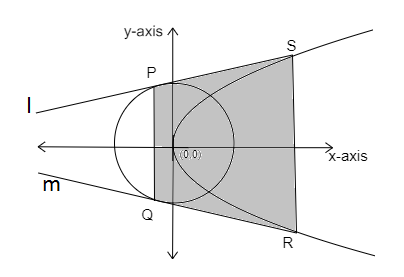
Figure: circle, parabola, and required quadrilateral PQRS
Let Tangents l and m are the common tangents to the circle and parabola.
Points P and Q are the points of contact of tangents l and m on the given circle.
Points R and S are the points of contact of tangents l and m on the given parabola.
Let the coordinates of point P $ = \left( {{x_1},{y_1}} \right)$
and the coordinate of point S $ = \left( {{x_2},{y_2}} \right)$
Given Equation of the circle ${x^2} + {y^2} = 2$
The point $P\left( {{x_1},{y_1}} \right)$ lies on the circle, therefore it must satisfy the equation of the circle, which means replace the coordinates \[\left( {x,y} \right)\] in the equation with the point $P\left( {{x_1},{y_1}} \right)$ .
Hence, \[{x_1}^2 + {y_1}^2 = 2\]
$ \Rightarrow {y_1}^2 = 2 - {x_1}^2$ …… (1)
The slope of a tangent to the circle:
i.e. differentiation of the equation of the circle with respect to x
${x^2} + {y^2} = 2$
\[\dfrac{d}{{dx}}\left( {{x^2} + {y^2}} \right) = \dfrac{d}{{dx}}\left( 2 \right)\]
$ \Rightarrow 2x + 2y\dfrac{{dy}}{{dx}} = 0$
$ \Rightarrow \dfrac{{dy}}{{dx}} = \dfrac{{ - 2x}}{{2y}}$
$ \Rightarrow \dfrac{{dy}}{{dx}} = \dfrac{{ - x}}{y}$
The slope of the tangent at the point of contact $P\left( {{x_1},{y_1}} \right)$
$ \Rightarrow {\dfrac{{dy}}{{dx}}_{\left( {{x_1},{y_1}} \right)}} = \dfrac{{ - {x_1}}}{{{y_1}}}$

Given Equation of parabola ${y^2} = 8x$
The point $S\left( {{x_2},{y_2}} \right)$ lies on the parabola, therefore it must satisfy the equation of the parabola, which means replace the coordinates \[\left( {x,y} \right)\] in the equation with the point $S\left( {{x_2},{y_2}} \right)$ .
Hence, ${y_2}^2 = 8{x_2}$ …… (2)
The slope of a tangent to the parabola:
i.e. differentiation of the equation of the parabola with respect to x
${y^2} = 8x$
\[\dfrac{d}{{dx}}\left( {{y^2}} \right) = \dfrac{d}{{dx}}\left( {8x} \right)\]
$ \Rightarrow 2y\dfrac{{dy}}{{dx}} = 8$
$ \Rightarrow \dfrac{{dy}}{{dx}} = \dfrac{8}{{2y}}$
$ \Rightarrow \dfrac{{dy}}{{dx}} = \dfrac{4}{y}$
The slope of the tangent at the point of contact $S\left( {{x_2},{y_2}} \right)$
$ \Rightarrow {\dfrac{{dy}}{{dx}}_{\left( {{x_2},{y_2}} \right)}} = \dfrac{4}{{{y_2}}}$
As the tangent to circle and parabola is common (i.e. same tangent line), therefore their slope must be the same.
Thus equating both the slopes
$ \Rightarrow \dfrac{{ - {x_1}}}{{{y_1}}} = \dfrac{4}{{{y_2}}}$
$ \Rightarrow {y_2} = \dfrac{{ - 4{y_1}}}{{{x_1}}}$ …… (3)
Substitute the value of ${y_2}$ from equation (3) in equation (2).
${y_2}^2 = 8{x_2}$
Substituting:
$ \Rightarrow {\left( {\dfrac{{ - 4{y_1}}}{{{x_1}}}} \right)^2} = 8{x_2}$
Simplifying:
$ \Rightarrow \dfrac{{16{y_1}^2}}{{{x_1}^2}} = 8{x_2}$
$ \Rightarrow {x_2} = \dfrac{{2{y_1}^2}}{{{x_1}^2}}$ ….. (4)
Step 2: Find the points of contacts, P, Q, R, and S.
Point $P\left( {{x_1},{y_1}} \right)$ and $S\left( {{x_2},{y_2}} \right)$ lies on a straight line, l
Thus, the slope of line l $ = \dfrac{{{y_2} - {y_1}}}{{{x_2} - {x_1}}}$
Also, the Slope of line l $ = \dfrac{{ - {x_1}}}{{{y_1}}}$
Thus, equating both the slopes.
$ \Rightarrow \dfrac{{{y_2} - {y_1}}}{{{x_2} - {x_1}}} = \dfrac{{ - {x_1}}}{{{y_1}}}$
$ \Rightarrow {y_1}\left( {{y_2} - {y_1}} \right) = - {x_1}\left( {{x_2} - {x_1}} \right)$
There are four unknowns present in the above equation.
Substituting ${x_{2,}},{y_2}$ from (4) and (3). Thus the equation becomes:
$ \Rightarrow {y_1}\left( {\dfrac{{ - 4{y_1}}}{{{x_1}}} - {y_1}} \right) = - {x_1}\left( {\dfrac{{2{y_1}^2}}{{x{{{}_1}^2}}} - {x_1}} \right)$
On further simplifying:
Take L.C.M. on both sides.
$ \Rightarrow {y_1}\left( {\dfrac{{ - 4{y_1} - {x_1}{y_1}}}{{{x_1}}}} \right) = - {x_1}\left( {\dfrac{{2{y_1}^2 - x{{{}_1}^2}}}{{x{{{}_1}^2}}}} \right)$
Cross multiplying of ${x_1}$ from left to right.
$ \Rightarrow {y_1}\left( { - 4{y_1} - {x_1}{y_1}} \right) = - {x_1}^2\dfrac{{\left( {2{y_1}^2 - x{{{}_1}^3}} \right)}}{{{x_1}^2}}$
$ \Rightarrow {y_1}\left( { - 4{y_1} - {x_1}{y_1}} \right) = - \left( {2{y_1}^2 - x{{{}_1}^3}} \right)$
On the left side take ${y_1}$ and on the right side take $ - $ minus sign inside the brackets. The brackets (or braces ) $\left( {} \right)$ , implies multiplication.
$ \Rightarrow \left( { - 4{y_1}^2 - {x_1}{y_1}^2} \right) = \left( { - 2{y_1}^2 + x{{{}_1}^3}} \right)$
Take all the variables on one side (preferably on the left side)
$ \Rightarrow x{{}_1^3} - 2{y_1}^2 + 4{y_1}^2 + {x_1}{y_1}^2 = 0$
$ \Rightarrow x{{}_1^3} + 2{y_1}^2 + {x_1}{y_1}^2 = 0$
The above equation is still in two variables. Substitute the value of \[{y_1}^2\] from the equation (1).
${y_1}^2 = 2 - {x_1}^2$
$ \Rightarrow x{{}_1^3} + 2\left( {2 - {x_1}^2} \right) + {x_1}\left( {2 - {x_1}^2} \right) = 0$
Multiplying and simplifying further:
$ \Rightarrow x{{}_1^3} + 4 - 2{x_1}^2 + 2{x_1} - {x_1}^3 = 0$
$ \Rightarrow 4 - 2{x_1}^2 + 2{x_1} = 0$
$ \Rightarrow {x_1}^2 - {x_1} - 2 = 0$
Using the middle term splitting method:
$ \Rightarrow {x_1}^2 - 2{x_1} + {x_1} - 2 = 0$
$ \Rightarrow {x_1}\left( {{x_1} - 2} \right) + 1\left( {{x_1} - 2} \right) = 0$
$ \Rightarrow \left( {{x_1} - 2} \right)\left( {{x_1} + 1} \right) = 0$
$\because {x_1} = - 1,{\text{ }}2$
Now find the values of the other remaining coordinates using the equations (1).
We have ${y_1}^2 = 2 - {x_1}^2$
Put ${x_1} = - 1$
$
  {y_1}^2 = 2 - {\left( { - 1} \right)^2} \\
   \Rightarrow 2 - 1 \\
   \Rightarrow 1 \\
$
$
  {y_1} = \sqrt 1 \\
   \Rightarrow \pm 1 \\
$
Hence point P $ = \left( { - 1,1} \right)$
And point Q $ = \left( { - 1, - 1} \right)$
Using ${x_1},{y_1}$ find value of ${x_2},{y_2}$
Put ${x_1} = - 1,{y_1} = 1$
We have ${x_2} = \dfrac{{2{y_1}^2}}{{{x_1}^2}}$ from equation (4).
$
  {x_2} = \dfrac{{2{{\left( 1 \right)}^2}}}{{{{\left( { - 1} \right)}^2}}} \\
   \Rightarrow 2 \\
$
We have ${y_2} = \dfrac{{ - 4{y_1}}}{{{x_1}}}$ from equation (3).
$
   \Rightarrow {y_2} = \dfrac{{ - 4\left( 1 \right)}}{{\left( { - 1} \right)}} \\
   \Rightarrow 4 \\
$
Hence, point S $ = \left( {2,4} \right)$
And Point R \[ = \left( {2, - 4} \right)\]
Step 3: Find the required area:
The required quadrilateral PQRS is a trapezium in shape.
With PQ and RS as parallel sides.
Line PQ is a vertical line on the x-axis. Point P is 1 unit above the x-axis and point Q is 1 unit below the x-axis. Thus the Length PQ $ = 2{\text{ units}}$(i.e. 1 + 1).
Line SR is a vertical line on the x-axis. The point S is 4 units above the x-axis and point R is also 4 units above the x-axis. Thus the length RS$ = 8{\text{ units}}$ (i.e. 4 + 4).
Lines PQ and RS are parallel lines. The x-coordinates of point P and Q are 1 unit left of the y-axis. The x-coordinates of S and R are 3 units right of the y-axis. Thus, the distance between parallel lines PQ and RS $ = 3{\text{ units}}$
Area of trapezium $ = \dfrac{1}{2}\left( {{\text{sum of length of two parallel sides}}} \right) \times \left( {{\text{distance between the parallel lines}}} \right)sq.units$
$
   \Rightarrow \dfrac{1}{2} \times \left( {2 + 8} \right) \times 3 \\
   \Rightarrow \dfrac{1}{2} \times 10 \times 3 \\
   \Rightarrow 15{\text{ sq}}{\text{.units}} \\
$

The required area of parallelogram PQRS is 15 sq. units. Thus, the correct option is (D).

Note: Solved these types of questions by obtaining the equation of the tangent to the curves.
To obtain the equation of the common tangent to the curves, equate the slopes of the tangents to the curves, obtained by differentiating the equation of the curves.
The equation of a line can also be obtained by point-slope form.
In point-slope form equation would be $y - {y_1} = m\left( {x - {x_1}} \right)$ here, x and y are variables of line and ${x_1}$ , ${y_1}$ is point on the line i.e. point satisfying the equation of the line.
Points P and Q come out to be (-1,1) and (-1,-1) i.e. both are equidistant from the y-axis (as x-coordinates are equal) which implies that line PQ is parallel to the y-axis, also S and R comes out to be (2,4) and (2,-4) i.e. both are also equidistant from the y-axis (as x-coordinates are equal) which implies line SR is parallel to the Y-axis. i.e. PQ and SR are parallel.
Obtain the area of the trapezium formed by joining P, Q, R, and S.
The slope of a line is also the tangent of the angle between the line and the positive direction of the x-axis.
Students may get mistaken that there will be only one common tangent to the circle and parabola but there are two common tangents as both are symmetrical figures.
Always remember while calculating the square-root of a number considers both the positive as well as a negative value. For example:
$
  {x^2} = 4 \\
  x = \sqrt 4 \\
  x = \pm 2 \\
$