Question

The centripetal force required for a 1000 kg car travelling at 36kmph to take a turn by ${90^ \circ }$ in traveling along an arc of length 628m is
A. 250 N
B. 500 N
C. 1000 N
D. 125 N

Answer 1

Hint: A centripetal force is a force that makes a body follow a curved path. The direction is always orthogonal to the motion of the body and towards the fixed point of the instantaneous centre of curvature of the path. It is basically the force that keeps the body moving around a fixed point.

Complete step-by-step answer:
In non-ideal cases, the circular motion of a body will not have constant angular velocity but it will slow down or pick up pace regularly. The total acceleration of a body moving in a circular motion is the resultant of two types of accelerations, namely Centripetal and Tangential acceleration.
$\overrightarrow a = {\overrightarrow a _c} + {\overrightarrow a _t}$
Let us consider a non-uniform circular motion as shown:

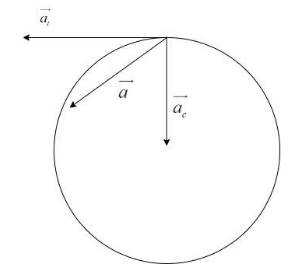
In a non-uniform circular motion, the body not only changes its angular velocity per unit time but also, the direction of the velocity vector. Since the velocity vector, which is a tangent to the direction of motion of the body, keeps changing every second, we get an additional component of acceleration. This component of acceleration is called Tangential acceleration.
Tangential acceleration, $\left| {{a_t}} \right| = r\alpha $
$\alpha $is called the angular acceleration, which means the change in angular velocity in radians per second.
$\alpha = \dfrac{\omega }{t}$
There is one more component of acceleration, for the actual change in the velocity per unit time and is directed towards the center of the circle. This is called Centripetal acceleration. This is also called Radial acceleration.
Centripetal acceleration ,$\left| {{a_c}} \right| = \dfrac{{{v^2}}}{r}$
The force associated with its centripetal acceleration is called centripetal force. It is equal to the mass times the centripetal acceleration.
${F_c} = m{a_c} = \dfrac{{m{v^2}}}{r}$
In the problem, given –
Mass, m = 1000 kg
Velocity, v = 36 kmph = $36 \times \dfrac{5}{{18}} = 10m{s^{ - 1}}$
Arc length, $l = 628m$
Arc length, $l = r\theta $
Given $\theta = {90^ \circ } = \dfrac{\pi }{2}rad$
Substituting, we get the radius of the turn, $r = \dfrac{l}{\theta } = \dfrac{{628 \times 2}}{{3.14}} = 400m$
Substituting in the equation for force, we get –
$
  {F_c} = \dfrac{{m{v^2}}}{r} \\
  {F_c} = \dfrac{{1000 \times {{10}^2}}}{{400}} = 250N \\
 $

Therefore, the correct option is Option A.

Note: In this problem, for the calculation of the radius, we used the Arc Length Formula.
Arc length formula is used to calculate the measure of the distance along the curved line making up an arc. The arc makes an angle known as $\theta $ at the centre of curvature in radians.
So, the arc length, $s = r\theta $ where r is called the radius of curvature.
It is important that the angle remains in radians and not in degrees.