Question

The area of two similar triangles are 81 sq. cm and 49 sq. cm respectively. Find the ratio of their corresponding heights. What is the ratio of their corresponding medians?

Answer 1

Hint: Here, we need to find the ratio of the corresponding heights and medians of the two triangles. First, we will find the ratio of the corresponding sides of the two triangles using the ratio of their areas. Then, we will use the formula of area of the two triangles and divide them to find the ratio of their corresponding heights. Finally, we will use similarity of the triangles that have the corresponding medians as a side, and use it to find the ratio of their corresponding medians.

Formula Used:
We will use the formula of the area of a triangle is given by the formula \[\dfrac{1}{2}bh\], where \[b\] is the base of the triangle, and \[h\] is the height of the triangle.

Complete step-by-step answer:
First, we will draw the two triangles with their heights.

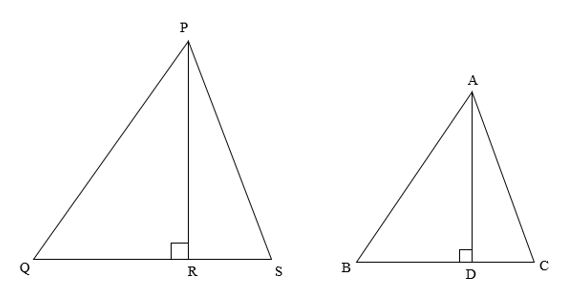
Here, AD is the height/altitude of triangle ABC, and PR is the height of triangle PQS. The triangle PQS has the area 81 sq. cm, and the triangle ABC has the area 49 sq. cm.
Now, it is given that the two triangles are similar.
The ratio of the areas of two similar triangles is the square of the ratio of any pair of corresponding sides of the two triangles.
Therefore, taking the corresponding sides QS and BC, we get
(Area of triangle PQS \[ \div \] Area of triangle ABC) \[ = {\left( {\dfrac{{QS}}{{BC}}} \right)^2}\]
Substituting area of triangle PQS as 81 sq. cm, and area of triangle ABC as 49 sq. cm, we get
\[ \Rightarrow \dfrac{{81}}{{49}} = {\left( {\dfrac{{QS}}{{BC}}} \right)^2}\]
Taking the square root on both the sides, we get
\[\begin{array}{l} \Rightarrow \sqrt {\dfrac{{81}}{{49}}} = \sqrt {{{\left( {\dfrac{{QS}}{{BC}}} \right)}^2}} \\ \Rightarrow \dfrac{{\sqrt {81} }}{{\sqrt {49} }} = \dfrac{{QS}}{{BC}}\end{array}\]
Simplifying the expression, we get
\[ \Rightarrow \dfrac{{QS}}{{BC}} = \dfrac{9}{7}\]
Thus, we get
\[ \Rightarrow \dfrac{{PQ}}{{AB}} = \dfrac{{QS}}{{BC}} = \dfrac{{PS}}{{AC}} = \dfrac{9}{7}\]
The area of a triangle is given by the formula \[\dfrac{1}{2}bh\], where \[b\] is the base of the triangle, and \[h\] is the height of the triangle.
Thus, we get
Area of triangle PQS \[ = \dfrac{1}{2} \times QS \times PR\]
Area of triangle ABC \[ = \dfrac{1}{2} \times BC \times AD\]
Dividing the two equations, we get
\[ \Rightarrow \] (Area of triangle PQS \[ \div \] Area of triangle ABC) \[ = \dfrac{{\dfrac{1}{2} \times QS \times PR}}{{\dfrac{1}{2} \times BC \times AD}}\]
Substituting area of triangle PQS as 81 sq. cm, and area of triangle ABC as 49 sq. cm, we get
\[ \Rightarrow \dfrac{{81}}{{49}} = \dfrac{{\dfrac{1}{2} \times QS \times PR}}{{\dfrac{1}{2} \times BC \times AD}}\]
Simplifying the expression, we get
\[\begin{array}{l} \Rightarrow \dfrac{{81}}{{49}} = \dfrac{{QS \times PR}}{{BC \times AD}}\\ \Rightarrow \dfrac{{81}}{{49}} = \dfrac{{QS}}{{BC}} \times \dfrac{{PR}}{{AD}}\end{array}\]
Substituting \[\dfrac{{QS}}{{BC}} = \dfrac{9}{7}\] in the equation, we get
\[ \Rightarrow \dfrac{{81}}{{49}} = \dfrac{9}{7} \times \dfrac{{PR}}{{AD}}\]
Multiplying both sides of the equation by \[\dfrac{7}{9}\], we get
\[\begin{array}{l} \Rightarrow \dfrac{{81}}{{49}} \times \dfrac{7}{9} = \dfrac{9}{7} \times \dfrac{{PR}}{{AD}} \times \dfrac{7}{9}\\ \Rightarrow \dfrac{9}{7} = \dfrac{{PR}}{{AD}}\end{array}\]
Thus, we get the ratio of the heights/altitude PR and AD as \[9:7\].
Now, we will draw the two triangles showing their medians.

Here, PT is the median of triangle PQS on the side QS, and AE is the median of triangle ABC to side BC.
Therefore, T is the midpoint of QS, and E is the midpoint of BC.
Thus, we get
\[QT = TS = \dfrac{1}{2}QS\]
and
\[BE = EC = \dfrac{1}{2}BC\]
Multiplying both sides of the equations by 2, we get
\[ \Rightarrow 2QT = 2TS = QS\]
 and
\[ \Rightarrow 2BE = 2EC = BC\]
The corresponding sides of two similar triangles are in equal ratio.
Therefore, since triangles PQS and ABC are similar, we get
\[ \Rightarrow \dfrac{{PQ}}{{AB}} = \dfrac{{QS}}{{BC}}\]
Substituting \[QS = 2QT\] and \[BC = 2BE\] in the equation, we get
\[ \Rightarrow \dfrac{{PQ}}{{AB}} = \dfrac{{2QT}}{{2BE}}\]
Simplifying the expression, we get
\[ \Rightarrow \dfrac{{PQ}}{{AB}} = \dfrac{{QT}}{{BE}}\]
Now, in triangles PQT and ABE, we get
\[\angle Q = \angle B\] (The angles of the similar triangle PQS and ABC are equal)
\[\dfrac{{PQ}}{{AB}} = \dfrac{{QT}}{{BE}}\]
Therefore, by S.A.S. similarity criterion, we have proved that triangles PQT and ABE are similar.
Since the corresponding sides of two similar triangles are in equal ratio, we get
\[ \Rightarrow \dfrac{{PQ}}{{AB}} = \dfrac{{QT}}{{BE}} = \dfrac{{PT}}{{AE}}\]
Substituting \[\dfrac{{PQ}}{{AB}} = \dfrac{9}{7}\] in the equation, we get
\[ \Rightarrow \dfrac{{QT}}{{BE}} = \dfrac{{PT}}{{AE}} = \dfrac{9}{7}\]
Thus, we get the ratio of the medians PT and AE as \[9:7\].
Note: We used the S.A.S. criterion of similarity to prove that the triangles ABD and PQT are similar. According to the S.A.S. similarity criterion, two triangles are similar if one of their angles is equal, and the ratio of the corresponding sides forming the equal angle is also equal.
We have used the terms ‘altitude’ and ‘median’ in the solution. An altitude is a line drawn from a vertex of a triangle to the opposite side, which is perpendicular to the opposite side. A median is a line drawn from a vertex of a triangle to the opposite side, which divides the opposite side into two equal parts.