Question

The area of the shaded region in the adjoining figure if every circle is of unit radius is

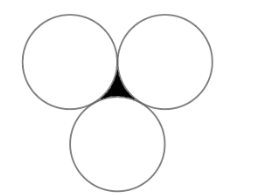
A. $\left( \sqrt{3}-\dfrac{\pi }{2} \right)sq.units$
B. $\left( \sqrt{3}+\pi \right)sq.units$
C. $\left( 2\sqrt{3}-\dfrac{\pi }{2} \right)sq.units$
D. $\left( \sqrt{3}-\dfrac{\pi }{4} \right)sq.units$

Answer 1

Hint: We will join the centre of each circle and we will get an equilateral triangle. Now, we will subtract the area of the sector from the area of the triangle to get the required area of the shaded region. We will use the formula of area of an equilateral triangle and area of a sector which is as follows;
Area of equilateral triangle $=\dfrac{\sqrt{3}}{4}{{a}^{2}}$, where ‘d’ is the side of the triangle.
Area of sector $=\pi {{r}^{2}}\times \left( \dfrac{\theta }{360{}^\circ } \right)$, where $'\theta '$ is the angle subtended by the arc corresponding to the sector.

Complete step-by-step answer:

Let us suppose the centre of the given circle to be A, B and C.

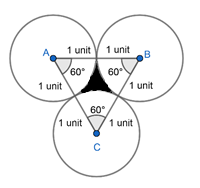
We get an equilateral $\Delta ABC$ having each side equal to 2 units, and each angle is equal to $60{}^\circ $.
To find the area of the shaded region we will have to subtract the area of all the three sectors from the area of the triangle.
We know that area of an equilateral triangle $=\dfrac{\sqrt{3}}{4}{{a}^{2}}$, where ‘a’ is the side of a triangle.
$\begin{align}
  & Area\ of\ \Delta ABC=\dfrac{\sqrt{3}}{4}\times {{\left( 2 \right)}^{2}} \\
 & =\dfrac{\sqrt{3}}{4}\times 4 \\
 & =\sqrt{3}sq.units \\
\end{align}$
Also, we know that area of sector of a circle is equal to $\pi {{r}^{2}}\times \left( \dfrac{\theta }{360{}^\circ } \right)$, where $'\theta '$ is the angle subtended at centre by arc corresponding to the sector.
Since, we have r = 1 unit and $\theta =60{}^\circ $.
$\begin{align}
  & \Rightarrow \text{Area of each sector }=\pi \times {{\left( 1 \right)}^{2}}\times \dfrac{60{}^\circ }{360} \\
 & =\dfrac{\pi }{6}sq.unit \\
 & \Rightarrow \text{Area of 3 sector }=3\times \dfrac{\pi }{6} \\
 & =\dfrac{\pi }{2}sq.unit \\
\end{align}$
Now, Area of shaded region = Area of equilateral triangle – Area of all 3 sectors
$=\left( \sqrt{3}-\dfrac{\pi }{2} \right)sq.units$
Therefore, the correct option of the given question is option A.

Note: For this type of questions, students must always use this approach of drawing an equilateral triangle through the centre of circles as only the radius is given to us. Remember that each angle of an equilateral triangle is equal to $60{}^\circ $ and also all sides are equal to each other.
Also, be careful while finding the area of the sector. Sometimes by mistake we use the radius of the circle as 2 units which is wrong and thus gives the incorrect answer.