Question

The area of the base of cone is 616 $cm^2$ and its height is 48 cm. the total surface area of the cone is
A. $ 2816\;c{m^2} $
B. $ 2861\;c{m^2} $
C. $ 2618\;c{m^2} $
D. $ 2681\;c{m^2} $

Answer 1

Hint: We have the base area of the cone and its height. To find the total surface area of the cone we have firstly calculate the radius of the cone. We calculate it from the base area of the cone. Once we calculate the base area then we calculate the slant height of the cone. Slant height is calculated with the help of radius and height of the cone. After calculating all this we use the formula of total surface area of cones. This will give us the required answer.

Complete step-by-step answer:
We have given height of cone (h) = 48 cm
base area of the cone = 616 $cm^2$
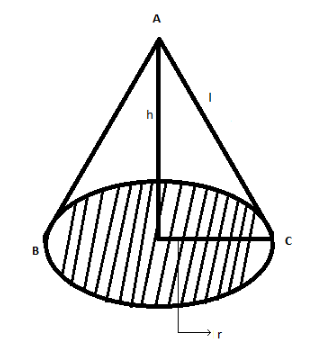
The shaped region shows the base area of the cone. Let r be the radius and l be the slant height of the cone.
Firstly we calculate radius of cone, base area of cone = 616 $cm^2$
\[ = \pi {r^2}\]Since the shape of the base of the cone is a circle. So, base area of cone = Area of circle

Therefore $ \pi {r^2} = 616 $ ; $ \pi = \dfrac{{22}}{7} $
Therefore $ \dfrac{{22}}{7} \times {r^2} = 616 $
 $ \Rightarrow {r^2} = 616 \times \dfrac{7}{{22}} $
 $ {r^2} = 28 \times 7 $
 $ r = \sqrt {196} = 14 $
So, radius of cone = 14 cm
Now we calculate the slant height of the cone.
Slant height of cone $ = \sqrt {{r^2} + {h^2}} $
 $ l = \sqrt {{{14}^2} + {{48}^2}} = \sqrt {196 + 2304} = \sqrt {2500} = 50 $
So, slant height of the cone is = 50cm
Now, we have to calculate the total surface area of the cone.
Total surface area of cone = curved surface area +base area of cone
 $ = \pi rl + \pi {r^2} $
 $ = \pi r(l + r) $
 $ = \dfrac{{22}}{7} \times 14(50 + 14) = \dfrac{{22}}{7} \times 14 \times 64 $
 $ = 2816\;c{m^2} $
So, the correct answer is “Option A”.

Note: Cone is a three dimensional solid structure that has a circular base. A cone can be viewed as a set of non- congruent circular disks that are placed over one another in such a way that the ratio of the radius of adjacent disk remains constant.