
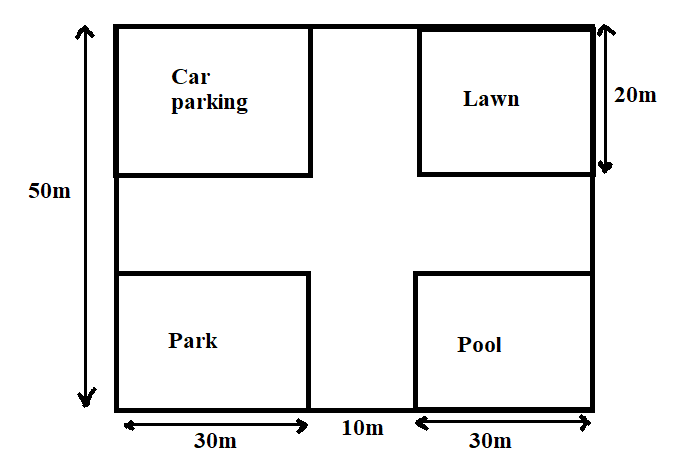
The area of car parking, lawn, swimming pool and park is the same. Find the area of the remaining portion.

Answer
587.4k+ views
Hint: We will first calculate the area of the rectangle ADIO and then subtract the area of the other four regions from the total area of the ADIO. The area of the rectangle ADIO is the product of its length and its breadth. Also, the area of the other four regions will be the same as they have the same dimensions.
Complete step-by-step answer:
We are given that the area of car parking, lawn, swimming pool and park is the same.
We have to find the area of the remaining portion.
From the diagram we will subtract the four areas, the car-parking area, lawn area, park area and pool area from the total area.

Required area is \[{\text{area of }}ADIO - {\text{area of}}\left( {{\text{ }}ABPN + CDEF + GHIJ + KLMO} \right)\]
Now, \[ADIO\] is a rectangle with length as 50m and breadth as $30m + 10m + 30m = 70m$
Also, the area of the rectangle is the product of the length and breadth.
Then, area of \[ADIO\] is $70 \times 50 = 3500{m^2}$
Next, the area of the other 4 rectangles will be the same as they all have length as 20m and breadth as 30m.
That is, $20 \times 30 = 600{m^2}$
Then, the required area is
$
3500 - \left( {600 + 600 + 600 + 600} \right) \\
3500 - \left( {2400} \right) \\
= 1100{m^2} \\
$
Hence, the area of the required area is $1100{m^2}$
Note: We can alternatively calculate the required area by adding the areas of KJGI, GHEF, BCFP, NPLM and PFGL, where area of the rectangle is the product of its length and breadth.
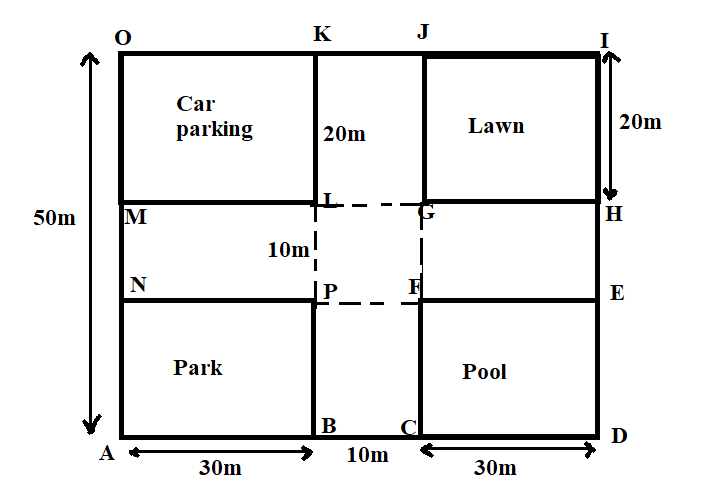
Complete step-by-step answer:
We are given that the area of car parking, lawn, swimming pool and park is the same.
We have to find the area of the remaining portion.
From the diagram we will subtract the four areas, the car-parking area, lawn area, park area and pool area from the total area.

Required area is \[{\text{area of }}ADIO - {\text{area of}}\left( {{\text{ }}ABPN + CDEF + GHIJ + KLMO} \right)\]
Now, \[ADIO\] is a rectangle with length as 50m and breadth as $30m + 10m + 30m = 70m$
Also, the area of the rectangle is the product of the length and breadth.
Then, area of \[ADIO\] is $70 \times 50 = 3500{m^2}$
Next, the area of the other 4 rectangles will be the same as they all have length as 20m and breadth as 30m.
That is, $20 \times 30 = 600{m^2}$
Then, the required area is
$
3500 - \left( {600 + 600 + 600 + 600} \right) \\
3500 - \left( {2400} \right) \\
= 1100{m^2} \\
$
Hence, the area of the required area is $1100{m^2}$
Note: We can alternatively calculate the required area by adding the areas of KJGI, GHEF, BCFP, NPLM and PFGL, where area of the rectangle is the product of its length and breadth.

Recently Updated Pages
Master Class 8 Social Science: Engaging Questions & Answers for Success

Master Class 8 English: Engaging Questions & Answers for Success

Class 8 Question and Answer - Your Ultimate Solutions Guide

Master Class 8 Maths: Engaging Questions & Answers for Success

Master Class 8 Science: Engaging Questions & Answers for Success

Master Class 9 General Knowledge: Engaging Questions & Answers for Success

Trending doubts
What is BLO What is the full form of BLO class 8 social science CBSE

Citizens of India can vote at the age of A 18 years class 8 social science CBSE

Full form of STD, ISD and PCO

Advantages and disadvantages of science

Right to vote is a AFundamental Right BFundamental class 8 social science CBSE

What are the 12 elements of nature class 8 chemistry CBSE




