Question

The area and perimeter of a protector with base 7cm are,

A. $6.5c{{m}^{2}}and\ 36cm$
B. $6.25c{{m}^{2}}and\ 36cm$
C. $6.125c{{m}^{2}}and\ 42cm$
D. $19.25c{{m}^{2}}and\ 18cm$

Answer 1

Hint: We know that area and circumference of a semicircle are equal to $\dfrac{\pi {{r}^{2}}}{2}$ and $\pi r$ respectively where ‘r’ is the radius of a circle. So, by using it we will get the required value of area and perimeter of the protector.

Complete step-by-step answer:
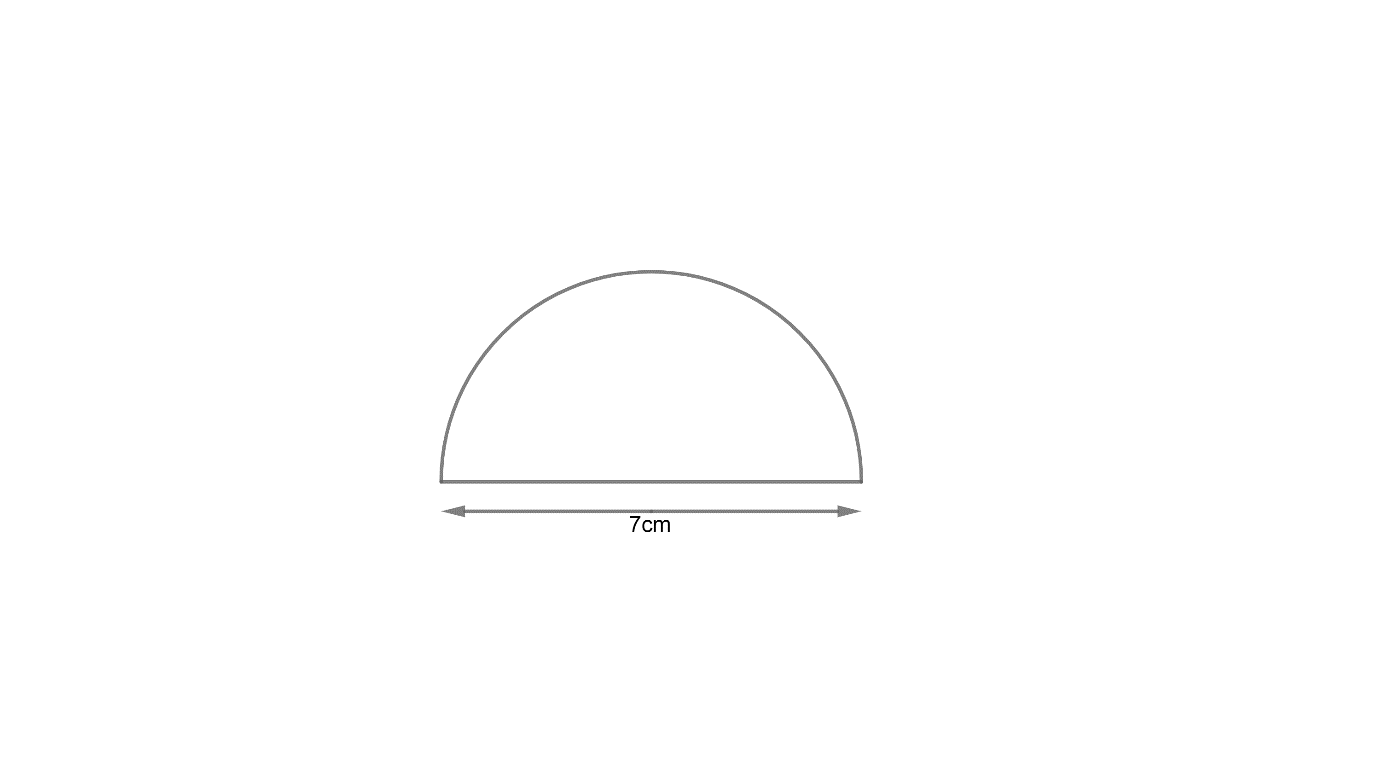
We have been the diameter of a protector is 7cm as show below:

Since, it is in the form of semicircle and we know that area and circumference of a semicircle are equal to $\dfrac{\pi {{r}^{2}}}{2}$ and $\pi r$ where ‘r’ is the radius of the semicircle.
We have radius $=\dfrac{7}{2}=3.5cm$, since, radius is half of the diameter.
Now, $area=\dfrac{\pi \times {{\left( 3.5 \right)}^{2}}}{2}c{{m}^{2}}$
Since, we know that $\pi =\dfrac{22}{7}$.
$\begin{align}
  & \Rightarrow area=\dfrac{22}{7}\times \dfrac{3.5\times 3.5}{2} \\
 & \Rightarrow area=\dfrac{38.5}{2}c{{m}^{2}} \\
 & \Rightarrow area=19.25c{{m}^{2}} \\
\end{align}$
Now, $circumference\left( C \right)=\pi r$
$\begin{align}
  & \Rightarrow C=\dfrac{22}{7}\times 3.5 \\
 & \Rightarrow C=11cm \\
\end{align}$
Since, we know that perimeter is the sum of the boundary of a geometrical figure. So, we must have to add the diametric length to the circumference of semicircle to get the perimeter of the protector which is in the form of semicircle.
$\begin{align}
  & \Rightarrow perimeter=c+d \\
 & =\left( 11+7 \right) \\
 & =18cm \\
\end{align}$
Hence, $area=19.25c{{m}^{2}}$and $perimeter=18cm$
Therefore, the correct option is D.
Note: Don’t get confused between the perimeter and the circumference of the semicircle, the perimeter includes all length i.e. the diameter length of semicircle also. So, be careful otherwise you will get incorrect answers i.e. 11 cm. Also, take care that we have been given the diameter of the protector so do not consider it like the radius of the protector.