Question

The angular points of a triangle are$A{\text{( - 1, - 7), }}B(5,1),{\text{ }}C(1,4).$The equation of bisector of angle
$\angle ABC$ is
$
  {\text{A}}{\text{. x}} = 7y + 2 \\
  {\text{B}}{\text{. }}7y = x + 2 \\
  {\text{C}}{\text{. }}y{\text{ = 7}}x{\text{ + 2}} \\
  {\text{D}}{\text{. 7}}x = y + 2 \\
 $

Answer 1

Hint: An angle bisector is a ray in the interior of an angle forming two congruent angles. In this problem you first need to find the coordinates of point $D$ which is on $AB$ using section formula and then find the equation of line $BD$.

Complete step-by-step answer:
 Let $ABC$ is triangle with coordinates $A{\text{( - 1, - 7), }}B(5,1),{\text{ }}C(1,4).$Since, we know that the angle bisector of a triangle divides the opposite side into two segments that are proportional to the other sides of the triangle.

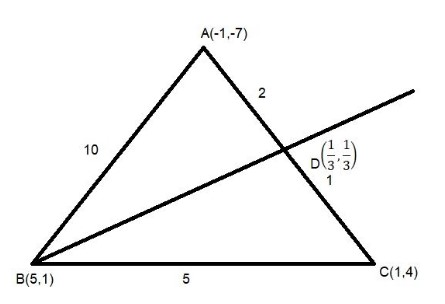
Since, the distance between two points is given by $\sqrt {{{({x_2} - {x_1})}^2} + {{({y_2} - {y_1})}^2}} $ where $({x_1},{y_1}){\text{ and }}({x_2},{y_2}){\text{ }}$are coordinates of two points.
Now, the length of $AB$
$
   \Rightarrow \sqrt {{{\{ 5 - ( - 1)\} }^2} + {{\{ 1 - ( - 7)\} }^2}} \\
   \Rightarrow \sqrt {{{(6)}^2} + {{(8)}^2}} \\
   \Rightarrow 10 \\
$
And, the length of $BC$
$
   \Rightarrow \sqrt {{{(1 - 5)}^2} + {{(4 - 1)}^2}} \\
   \Rightarrow \sqrt {{{( - 4)}^2} + {{(3)}^2}} \\
   \Rightarrow 5 \\
$
Now, the angular bisector of angle $\angle ABC$ is divides the opposite side $AC$ in ratio 10:5 or 2:1
By using Section Formula
If a point $P(x,y)$ divides the line joining two points $Q(a,b){\text{ and }}R(c,d)$ in the ratio $m:n$ internally, then the coordinates of $P(x,y)$ are given by
$ \Rightarrow P(x,y) = (\dfrac{{c.m + a.n}}{{m + n}},\dfrac{{d.m + b.n}}{{m + n}})$
Here $m=2$ , $n=1$ ,$A(-1,-7)$ and $C(1,4)$.
$ \Rightarrow P(x,y) = (\dfrac{{2.1 + 1.(-1)}}{{2 + 1}},\dfrac{{2.4 + 1.(-7)}}{{2 + 1}})$
Then, the coordinates of point $D$ on line $AB$
$
   \Rightarrow D = (\dfrac{{ 2 - 1}}{3},\dfrac{{ 8 - 7}}{3}) \\
   \Rightarrow D = (\dfrac{1}{3},\dfrac{1}{3}) \\
 $
Since, the equation of line passing through two given points is given by$y - {y_1} = (\dfrac{{{y_2} - {y_1}}}{{{x_2} - {x_1}}})(x - {x_1})$where $({x_1},{y_1}){\text{ and (}}{x_2},{y_2})$ are coordinates of two points
Then equation of angular bisector$(BD)$ of angle $\angle ABC$ is given by
 $
   \Rightarrow {\text{ }}y - 1 = \dfrac{{(1 - \dfrac{1}{3})}}{{(5 - \dfrac{1}{3})}}(x - 5) \\
   \Rightarrow y - 1 = \dfrac{2}{{14}}(x - 5) \\
   \Rightarrow 7(y - 1) = (x - 5) \\
   \Rightarrow x - 7y + 2 = 0 \\
   \Rightarrow x + 2 = 7y \\
$
Hence, option B is correct.

Note: Whenever you get this type of question the key concept of solving this is to have knowledge about angular bisector ,its properties , Section Formula, formation of equation of line using two points which is given by $y - {y_1} = (\dfrac{{{y_2} - {y_1}}}{{{x_2} - {x_1}}})(x - {x_1})$ and how to apply them. You should make a rough diagram of the question to get a better understanding.