Question

The angles in a right angled isosceles triangle are:
$
  (a){\text{ 6}}{{\text{0}}^0},{\text{ 6}}{{\text{0}}^0},{\text{ 6}}{{\text{0}}^0} \\
  (b){\text{ 9}}{{\text{0}}^0},{\text{ 6}}{{\text{0}}^0},{\text{ 3}}{{\text{0}}^0} \\
  (c){\text{ 9}}{{\text{0}}^0},{\text{ 4}}{{\text{5}}^0},{\text{ 4}}{{\text{5}}^0} \\
  (d){\text{ 7}}{{\text{0}}^0},{\text{ 5}}{{\text{0}}^0},{\text{ 6}}{{\text{0}}^0} \\
$

Answer 1

Hint – In this question use the concept that the angles opposite to equal sides are also equal, since it is an isosceles triangle thus two sides must be equal to each other in length.

Complete step-by-step answer:

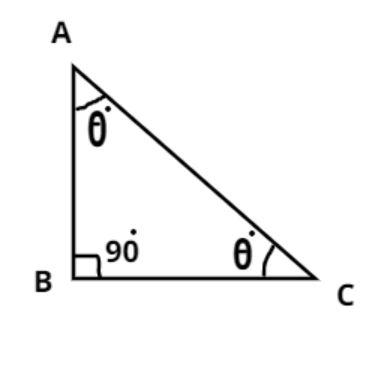
Let ABC be a right angled isosceles triangle as shown above, which is right angled at B.
$ \Rightarrow \angle B = {90^0}$.
And we know in an isosceles triangle two angles are equal such that AB=BC.
So let $\angle A = \angle C = \theta $ (Using the property that angles opposite to equal sides are equal)
And we know that in a triangle the sum of all the angles is 180 degrees.
$ \Rightarrow \angle A + \angle B + \angle C = {180^0}$
Now substitute the values in above equation we have,
\[ \Rightarrow \theta + {90^0} + \theta = {180^0}\]
Now simplifying the above equation we get,
\[ \Rightarrow 2\theta = {180^0} - {90^0} = {90^0}\]
$ \Rightarrow \theta = \dfrac{{{{90}^0}}}{2} = {45^0}$.
So the angles in a right isosceles triangle are ${90^0},{45^0},{45^0}$.
Hence option (C) is correct.

Note – Diagrammatic representation of triangles helps in understanding about the concept of isosceles triangle. In this question we have taken two sides as equal which are AB and BC and have not paired them with hypotenuses, because the length of hypotenuse is always greater than the rest sides hence we can’t make it equal to any other side of the triangle.