Question

Sum of the adjacent angles of a parallelogram is equal to
A) 60$^\circ $
B) 90$^\circ $
C) 150$^\circ $
D) 180$^\circ $

Answer 1

Hint- In this particular type of question, we need to draw a parallelogram and understand its geometry to write the desired answer. Using the properties of parallelograms we can find the solution for this problem.

Complete step-by-step answer:

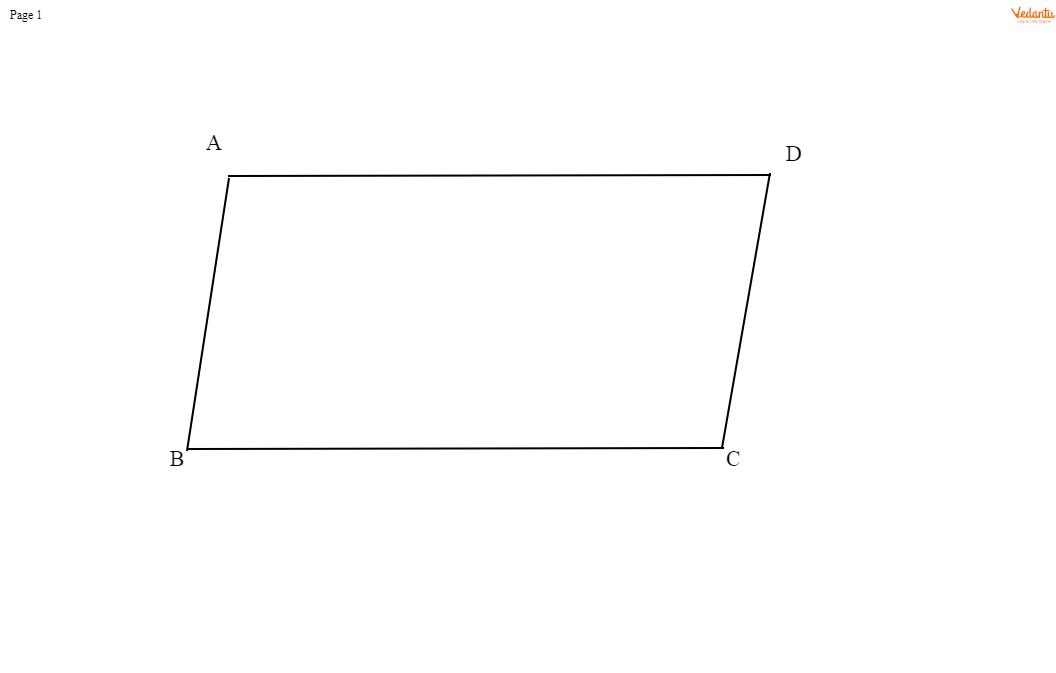
Two angles are Adjacent when they have a common side and a common vertex and don't overlap.
In the given figure quadrilateral ABCD is a parallelogram.
 Then, $AD\parallel BC$ and AB is transversal.
 A + B = $180^\circ $
 ( Interior angles on the same side of transversal are supplementary)
Angle A and B are adjacent angles as they have a common side. Therefore the sum of adjacent angles of a parallelogram is = A + B = $180^\circ $
So option (D) is correct.

Note- We have to remember to recall the basic properties of parallelograms. We should know that a parallelogram is a quadrilateral with two pairs of parallel sides. If we extend the sides of the parallelogram in both directions, we now have two parallel lines cut by two parallel transversals. And we know that when two parallel lines are cut by a transversal corresponding angles are equal in measure thus adjacent angles are supplementary.