Question

State which of the following pairs of triangles are congruent. If yes, write them in symbolic form (You may draw a rough figure).
 $ \Delta PQR:PQ = 3.5cm,QR = 4.0cm,\angle Q = {60^ \circ } $
 $ \Delta STU:ST = 3.5cm,TU = 4cm,\angle T = {60^ \circ } $

Answer 1

Hint: In this question, we have been given two sides and one angle. So we will first draw the figure and their measurements. Then we will check if these satisfy the SAS criteria or SAS congruence. The SAS congruence rule says that if two sides of the triangle and one given angle in a given triangle is equal to the other corresponding sides and angles of the another triangle, then the triangles are said to be congruent. We will denote it by the symbol $ \cong $ .

Complete step-by-step answer:
From the given data in the question we can see that we have two sides and angles of triangles. So the congruency criteria which consists of two sides and one angle is $ SAS $ Congruency.
Two prove two triangles are congruent by SAS criteria we need to check if the two sides and one included angle of one triangle is equal to the other corresponding triangle.
So let us first draw the diagram of both the triangles according to the data given in the question:

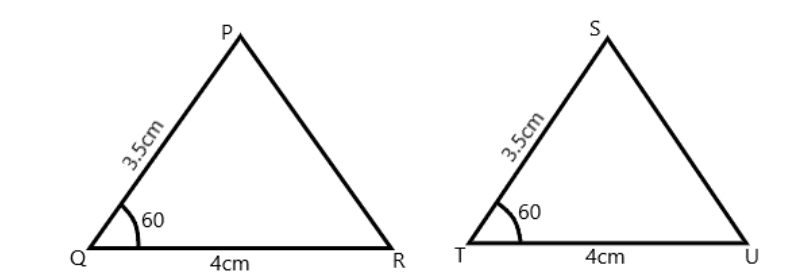
From the image above we can see that the two sides i.e.
 $ PQ,QR $ of one triangle is equal to the sides of another triangle i.e.
 $ ST,TU $ .
Now in the triangle PQR and triangle STU, we have
 $ PQ = ST = 3.5cm $
(Given in the question)
 $ QR = TU = 4cm $
(Given in the question)
And,
 $ \angle PQR = \angle STU = {60^ \circ } $ .
 (Given in the question)
We can see that the two sides and one triangle PQR are equal to the two sides and one angle of another triangle STU.
So we can say that both of these triangles are congruent by SAS criterion.
Hence we can write that , by SAS congruence rule $ \Delta PQR \cong \Delta STU $ .

Note: We should note that there are other rules of the congruency. The other ways are:
 $ SSS $ Congruence- It stands for Side, Side and Side criteria. If three sides of one triangle are equal to the three sides of another triangle, then they are congruent by SSS criteria.
 $ ASA $ Congruence- It stands for angle, side and angle. If two angles and the included side of one triangle is congruent to the two angles and included side of another triangle then the triangle is congruent by ASA criteria.
 $ AAS $ Congruence- It stands for angle, angle and side. If two angles and the non-included side of a triangle are equal to the corresponding sides and angles to another triangle, then we can say that both the triangles are congruent by AAS congruence.