Question

How many spheres of diameter 12cm each, can be made from a metallic cylinder of diameter 8cm? The height of the cylinder is 90cm.

Answer 1

Hint: Calculate the volume of the cylinder using the formula $\pi {{r}^{2}}h$, where ‘r’ is the radius of the sphere and ‘h’ is the height of the sphere. Calculate the volume of the sphere using the formula $\dfrac{4}{3}\pi {{r}^{3}}$, where ‘r’ is the radius of the sphere. Divide the volume of the cylinder by volume of the sphere to calculate the number of spheres that can be made from the cylinder.

Complete step-by-step answer:
We have to calculate the number of spheres that can be made from a cylinder when the dimensions of the sphere and cylinder are given. To do so, we will calculate the volume of both sphere and cylinder.
We know that the volume of the cylinder whose radius is ‘r’ and height is ‘h’ is $\pi {{r}^{2}}h$.
We know that the diameter of the cylinder is 8cm. We will calculate the radius of the cylinder by dividing the diameter by 2.
Thus, the radius of the cylinder $=\dfrac{8}{2}=4cm$. We know the height of the cylinder is 90cm.
 

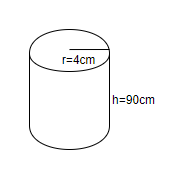
Thus, the volume of the cylinder is $=\pi {{\left( 4 \right)}^{2}}\left( 90 \right)=3.14\times 16\times 90=4521.6c{{m}^{3}}$.
We will now calculate the volume of the sphere. We know that the diameter of the sphere is 12cm.
We will calculate the radius of the sphere by dividing the diameter by 2.
Thus, the radius of the sphere $=\dfrac{12}{2}=6cm$.
We know that the volume of the sphere with radius ‘r’ is $\dfrac{4}{3}\pi {{r}^{3}}$.

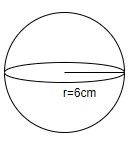
Thus, the volume of the sphere $=\dfrac{4}{3}\pi {{\left( 6 \right)}^{3}}=\dfrac{4}{3}\times 3.14\times 216=904.32c{{m}^{3}}$.
We will now calculate the number of spheres that can be made from the given cylinder. To do so, we will divide the volume of the cylinder by the volume of the sphere.
Thus, the number of spheres which can be made $=\dfrac{4521.6}{904.32}=5$.
Hence, we can make 5 spheres from the cylinder of the given dimensions.

Note: One must be careful about units while calculating the volume cylinder and sphere. One must also keep in mind that we have data regarding the diameter of the cylinder and sphere. So, we must convert it to the radius or we should use the formula for calculating volume using diameter. Also, the number of spheres is a dimensionless quantity.