Question

Sphere of radius R having charge q is joined to another conducting sphere of radius 2R having charge -2q. The charge flowing between them will be
(A) $q$
(B) $\dfrac{q}{3}$
(C) $\dfrac{{2q}}{3}$
(D) $\dfrac{{4q}}{3}$

Answer 1

Hint: Electric potential is defined as the amount of work needed to be done to move a unit charge from a reference point or from infinity to the point of interest against the electric field.
Electric potential is directly proportional to the charge $q$ and the inversely proportional to the distance which is traveled by the point charge to the reference position(r).

Formula used:
Electric potential $V=\dfrac{1}{{4\pi {\varepsilon _0}}}\dfrac{q}{r} = \dfrac{{kq}}{r}$ ; here q is the charge, r is the distance.

Complete step-by-step answer:
We know that the charge q and charge -2q are placed at the conducting spheres of radius R and 2R respectively. The Following is the diagram represents the arrangement of charges q and -2q in the space,

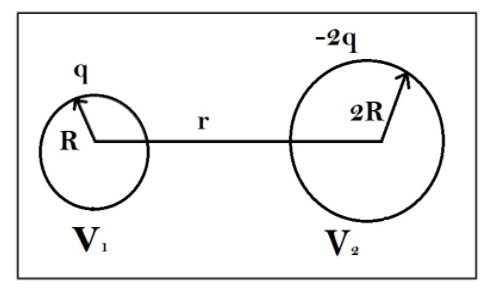
From the diagram, we know that both charges are connected through the common potential. Thus, the individual potentials i.e.\[{{\text{V}}_{\text{1}}}{\text{ and }}{{\text{V}}_{\text{2}}}\]are equal to each other.which can be shown as follows,
${V_1} = {V_2}$ ... equation (1)
So let us first find the individual potentials of the spheres. Let us consider that Q and Q’ are the charges on the two spheres. Then the potential can be found using the formula
$V = \dfrac{1}{{4\pi {\varepsilon _0}}}\dfrac{q}{r} = \dfrac{{kq}}{r}$.
Thus the potential for \[{{\text{V}}_{\text{1}}}{\text{ and }}{{\text{V}}_{\text{2}}}\] can be given as follows,
${V_1} = \dfrac{{kQ}}{R}$ And ${V_2} = \dfrac{{kQ'}}{{2R}}$
Let us substitute the values in equation (1). On substituting in the equation we get,
$\dfrac{{kQ}}{R} = \dfrac{{kQ'}}{{2R}}$
Let us simplify the above equation. On simplification we get,
$\dfrac{{kQ}}{R} - \dfrac{{kQ'}}{{2R}} = 0$
Let us further simplify it for Q we get,
$\dfrac{{2kQ - kQ'}}{{2R}} = 0 \Rightarrow Q = \dfrac{{Q'}}{2}$ …. equation (2)
Equation(2) gives us the relation between the charges of the sphere.
We can also write the total charge as following,
$Q+Q’=q-2q=-q$ ….. equation (3)
Now, let us find the charges Q and Q’ in terms of q by using the relation from (2) and (3). We get,
 $ \Rightarrow Q' = \dfrac{{ - 2q}}{3}$ and $Q = - \dfrac{q}{3}$ ….equation (4)
Now We have to find the charge flowing, which can be found by subtracting the initial charges on the sphere and the charge after applying a potential.
So let us find the difference of charge on the sphere of radius 2R and initial charge -2q, final charge Q= -\[2q/3\].
Thus, Charge flowing can be given as = $ - 2q - \left( {\dfrac{{ - 2q}}{3}} \right) = \dfrac{{ - 4q}}{3}$

$\therefore$ option (D) “\[\dfrac{{4q}}{3}\]” is the correct option.

Note:
When the spheres are connected by a conductive wire, the charge can move from one sphere to another. The sphere with higher potential will be partly discharged through the wire while charging the other ball. At the end of this process, both spheres will have the same potential.