
How do you solve the system of equations $2x-5y=-1$ and $4x-5y=13$ ?
Answer
538.5k+ views
Hint: We have been given two equations in two variables, x and y, which must be solved simultaneously as well as drawn on the same graph to find the solution of these equations. We will first find two points lying on each straight-line given by putting $x=0$ and $y=0$ one-by-one in each equation. Using these, we will further plot the graphs of these equations.
Complete step by step answer:
We will put the values of x and y equal to zero one by one to find two simple points one of which will have its x-coordinate equal to zero and the other one would have its y-coordinate equal to zero.
We shall first find the points lying on the line whose equation is given by, $2x-5y=-1$.
Putting $x=0$ in the equation, we get
$2\left( 0 \right)-5y=-1$
$\Rightarrow -5y=-1$
Now, we shall take divide both sides by -5 to find y:
$\begin{align}
& \Rightarrow y=\dfrac{-1}{-5} \\
& \Rightarrow y=\dfrac{1}{5} \\
\end{align}$
Therefore, we get the point as $\left( 0,\dfrac{1}{5} \right)$ .
Putting $y=0$ in the equation, we get
$2x-5\left( 0 \right)=-1$
$\Rightarrow 2x=-1$
Now, we shall divide both sides by 2 to find x:
$\Rightarrow x=\dfrac{-1}{2}$
Therefore, we get the point as $\left( -\dfrac{1}{2},0 \right)$
Hence, the points are $\left( 0,\dfrac{1}{5} \right)$and $\left( -\dfrac{1}{2},0 \right)$. …………………….. (1)
We shall now find the points on the second equation given as, $4x-5y=13$.
Putting $x=0$ in the equation, we get
$\begin{align}
& 4\left( 0 \right)-5y=13 \\
& \Rightarrow -5y=13 \\
\end{align}$
Dividing both sides by -5, we get
$\Rightarrow y=-\dfrac{13}{5}$
Therefore, we get the point as $\left( 0,-\dfrac{13}{5} \right)$.
Putting $y=0$ in the equation, we get
$\begin{align}
& 4x-5\left( 0 \right)=13 \\
& \Rightarrow 4x=13 \\
\end{align}$
Dividing both sides by 4, we get
$\Rightarrow x=\dfrac{13}{4}$
Therefore, we get the point as $\left( \dfrac{13}{4},0 \right)$.
Hence, the points are $\left( 0,-\dfrac{13}{5} \right)$and $\left( \dfrac{13}{4},0 \right)$ . ………………… (2)
From (1) and (2), we get the graph as:
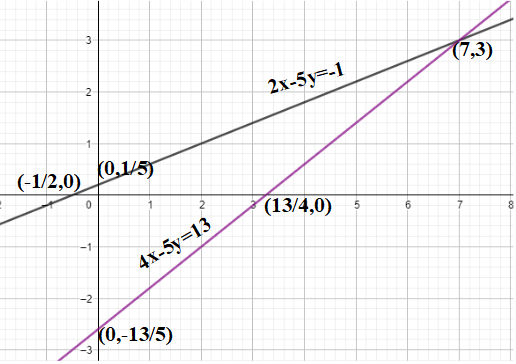
Therefore, the solution of the given system of equations is (7,3) as it is the point of intersection of the two straight-lines.
Note: While sketching any graph, the two points should always be taken such that the x or y coordinates are zero in them as it makes the calculations easier. While plotting the graph, the points must be marked with precision. One possible mistake we could have done was marking (0, 0.5) instead of (-0.5,0).
Complete step by step answer:
We will put the values of x and y equal to zero one by one to find two simple points one of which will have its x-coordinate equal to zero and the other one would have its y-coordinate equal to zero.
We shall first find the points lying on the line whose equation is given by, $2x-5y=-1$.
Putting $x=0$ in the equation, we get
$2\left( 0 \right)-5y=-1$
$\Rightarrow -5y=-1$
Now, we shall take divide both sides by -5 to find y:
$\begin{align}
& \Rightarrow y=\dfrac{-1}{-5} \\
& \Rightarrow y=\dfrac{1}{5} \\
\end{align}$
Therefore, we get the point as $\left( 0,\dfrac{1}{5} \right)$ .
Putting $y=0$ in the equation, we get
$2x-5\left( 0 \right)=-1$
$\Rightarrow 2x=-1$
Now, we shall divide both sides by 2 to find x:
$\Rightarrow x=\dfrac{-1}{2}$
Therefore, we get the point as $\left( -\dfrac{1}{2},0 \right)$
Hence, the points are $\left( 0,\dfrac{1}{5} \right)$and $\left( -\dfrac{1}{2},0 \right)$. …………………….. (1)
We shall now find the points on the second equation given as, $4x-5y=13$.
Putting $x=0$ in the equation, we get
$\begin{align}
& 4\left( 0 \right)-5y=13 \\
& \Rightarrow -5y=13 \\
\end{align}$
Dividing both sides by -5, we get
$\Rightarrow y=-\dfrac{13}{5}$
Therefore, we get the point as $\left( 0,-\dfrac{13}{5} \right)$.
Putting $y=0$ in the equation, we get
$\begin{align}
& 4x-5\left( 0 \right)=13 \\
& \Rightarrow 4x=13 \\
\end{align}$
Dividing both sides by 4, we get
$\Rightarrow x=\dfrac{13}{4}$
Therefore, we get the point as $\left( \dfrac{13}{4},0 \right)$.
Hence, the points are $\left( 0,-\dfrac{13}{5} \right)$and $\left( \dfrac{13}{4},0 \right)$ . ………………… (2)
From (1) and (2), we get the graph as:
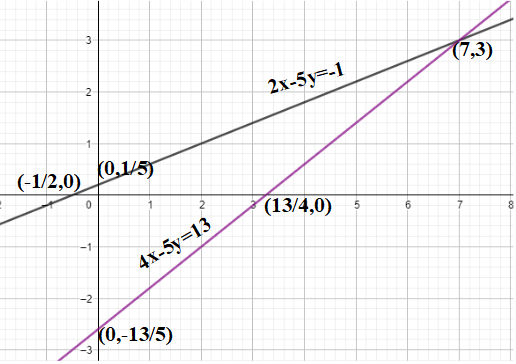
Therefore, the solution of the given system of equations is (7,3) as it is the point of intersection of the two straight-lines.
Note: While sketching any graph, the two points should always be taken such that the x or y coordinates are zero in them as it makes the calculations easier. While plotting the graph, the points must be marked with precision. One possible mistake we could have done was marking (0, 0.5) instead of (-0.5,0).
Recently Updated Pages
Master Class 9 Social Science: Engaging Questions & Answers for Success

Master Class 9 Science: Engaging Questions & Answers for Success

Master Class 9 English: Engaging Questions & Answers for Success

Master Class 9 Maths: Engaging Questions & Answers for Success

Master Class 11 Economics: Engaging Questions & Answers for Success

Master Class 11 English: Engaging Questions & Answers for Success

Trending doubts
Which places in India experience sunrise first and class 9 social science CBSE

Fill the blanks with the suitable prepositions 1 The class 9 english CBSE

Write the 6 fundamental rights of India and explain in detail

Difference Between Plant Cell and Animal Cell

What is the Full Form of ISI and RAW

Golden Revolution is related to AFood production BOil class 9 social science CBSE





