Question

How‌ ‌do‌ ‌you‌ ‌solve‌ ‌the‌ ‌system‌ ‌$2x+y=3$‌ ‌and‌ ‌$2x+y=-1$‌ ‌by‌ ‌graphing?‌

Answer 1

Hint: At first, we find two such points for each line that satisfy the corresponding lines. We plot the points on a graph and then join the corresponding points to get the lines. We will see that the two lines are parallel and thus, they don’t have any solution.

Complete step-by-step solution:
The two equations that we are given are
$2x+y=3....\left( 1 \right)$
$2x+y=-1....\left( 2 \right)$
To plot the above equations on a graph, we can see that the equations are those of straight lines. So, we will go for the two point method. In this method, we have to find two such points that lie on the line. The required line will be that one which joins these two points.
Keeping the above method in mind, let us find two such points that lie on the equation $\left( 1 \right)$ . They are $\left( 1,1 \right)$ and $\left( 0,3 \right)$ . We plot these two points on the graph. Using a scale, we join these two points and get the line. Following the same method, two such points that lie on the equation $\left( 2 \right)$ are $\left( 0,-1 \right)$ and $\left( -1,1 \right)$ . Using a scale, we join these two points to get the required line.

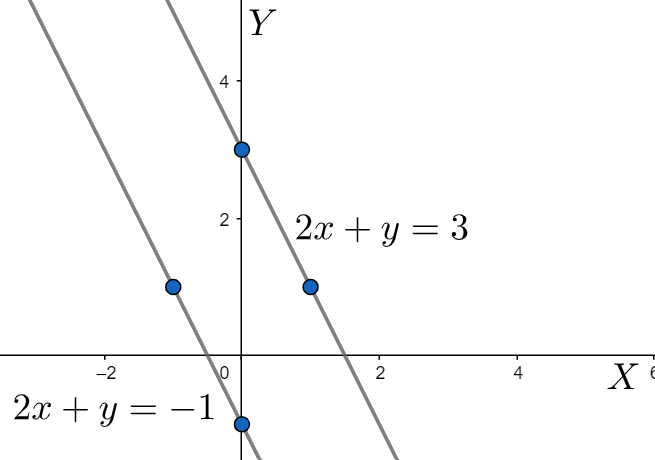
We can clearly see that the two lines do not intersect anywhere, or that they are parallel to each other. Parallel lines, not intersecting anywhere, have no point of intersection. This means that there is no such point which lies on both the lines. This means that there is no such point which satisfies both the equations at the same time. Or, we can say that the two equations do not have any solutions.
Therefore, we can conclude that the two given equations don’t have any solution.

Note: In this problem, we need to be careful while finding out the points that satisfy the equations, keeping the signs in mind or, we end up in different points and thus different lines. Also, we can use other techniques to draw the graph like the slope-intercept technique and the intercept form.