
Solve the pair of linear equations graphically.
$
2x + y - 6 = 0 \\
4x - 2y - 4 = 0 \\
$
Answer
569.7k+ views
Hint: To find a solution to a given linear equation graphically. We first take different values of either of one variable and then solve the other variable by the help of the given equation and then plot a graph of both equations on the same graph to find where both lines meet or we can say the solution of the given equations.
Complete step-by-step answer:
Given, linear equations are
$
2x + y - 6 = 0 \\
4x - 2y - 4 = 0 \;
$
To draw a graph of a given linear equation.
We take different values of either or of one variable and solve another variable using one variable.
We first consider an equation:
$2x + y - 6 = 0$
Taking $x = 1$ in above equation. We have
$
2(1) + y - 6 = 0 \\
\Rightarrow 2 + y - 6 = 0 \\
\Rightarrow y - 4 = 0 \\
\Rightarrow y = 4 \;
$
We have $\left( {1,4} \right)$
Taking $x = 2\,$we have,
$
2(2) + y - 6 = 0 \\
\Rightarrow 4 + y - 6 = 0 \\
\Rightarrow y - 2 = 0 \\
\Rightarrow y = 2 \;
$
We have $\left( {2,2} \right)$
Taking $x = 3$we have
$
2\left( 3 \right) + y - 6 = 0 \\
6 + y - 6 = 0 \\
y = 0 \;
$
We have $\left( {3,0} \right)$
Hence, table of values given as
Now, considering other equation:
$
4x - 2y - 4 = 0 \\
or\,\,we\,\,can\,\,write\,\,it\,\,as: \\
2x - y - 2 = 0 \;
$
Now take the different values of x in the above equation and solve for y.
Taking $x = 1$
$
2(1) - y - 2 = 0 \\
\Rightarrow 2 - y - 2 = 0 \\
\Rightarrow - y = 0 \\
\Rightarrow y = 0 \;
$
We have $\left( {1,0} \right)$
Taking $x = 2$
$
2(2) - y - 2 = 0 \\
\Rightarrow 4 - y - 2 = 0 \\
\Rightarrow 2 - y = 0 \\
\Rightarrow y = 2 \;
$
We have $\left( {2,2} \right)$
Taking $y = 3$
$
2(3) - y - 2 = 0 \\
\Rightarrow 6 - y - 2 = 0 \\
\Rightarrow 4 - y = 0 \\
\Rightarrow y = 4 \;
$
We have $\left( {3,4} \right)$
Hence, table of values given as:
Now plotting all points obtained in the x y plane to draw a graph of both equations.
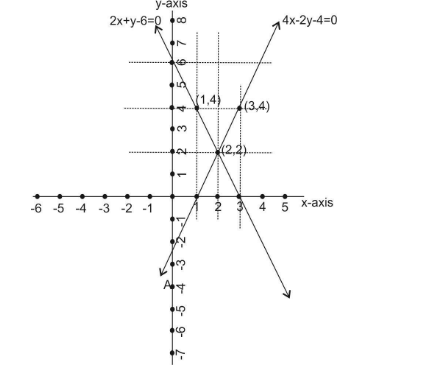
From the above graph we see that graphs of both lines intersect or meet at a point$\left( {2,2} \right)$.
Hence the solution of the given equation is$\left( {2,2} \right)$.
So, the correct answer is “{2,2} ”.
Note: While plotting deterrent points on x y plane if graph is not coming straight line then we can say that there is a mistake in calculations as we know that graph of linear equation is a straight line. Also, we can cross check graphs by putting points of intersection in given equations as points of intersection will satisfy both linear equations.
Complete step-by-step answer:
Given, linear equations are
$
2x + y - 6 = 0 \\
4x - 2y - 4 = 0 \;
$
To draw a graph of a given linear equation.
We take different values of either or of one variable and solve another variable using one variable.
We first consider an equation:
$2x + y - 6 = 0$
Taking $x = 1$ in above equation. We have
$
2(1) + y - 6 = 0 \\
\Rightarrow 2 + y - 6 = 0 \\
\Rightarrow y - 4 = 0 \\
\Rightarrow y = 4 \;
$
We have $\left( {1,4} \right)$
Taking $x = 2\,$we have,
$
2(2) + y - 6 = 0 \\
\Rightarrow 4 + y - 6 = 0 \\
\Rightarrow y - 2 = 0 \\
\Rightarrow y = 2 \;
$
We have $\left( {2,2} \right)$
Taking $x = 3$we have
$
2\left( 3 \right) + y - 6 = 0 \\
6 + y - 6 = 0 \\
y = 0 \;
$
We have $\left( {3,0} \right)$
Hence, table of values given as
| x | 1 | 2 | 3 |
| y | 4 | 2 | 0 |
Now, considering other equation:
$
4x - 2y - 4 = 0 \\
or\,\,we\,\,can\,\,write\,\,it\,\,as: \\
2x - y - 2 = 0 \;
$
Now take the different values of x in the above equation and solve for y.
Taking $x = 1$
$
2(1) - y - 2 = 0 \\
\Rightarrow 2 - y - 2 = 0 \\
\Rightarrow - y = 0 \\
\Rightarrow y = 0 \;
$
We have $\left( {1,0} \right)$
Taking $x = 2$
$
2(2) - y - 2 = 0 \\
\Rightarrow 4 - y - 2 = 0 \\
\Rightarrow 2 - y = 0 \\
\Rightarrow y = 2 \;
$
We have $\left( {2,2} \right)$
Taking $y = 3$
$
2(3) - y - 2 = 0 \\
\Rightarrow 6 - y - 2 = 0 \\
\Rightarrow 4 - y = 0 \\
\Rightarrow y = 4 \;
$
We have $\left( {3,4} \right)$
Hence, table of values given as:
| x | 1 | 2 | 3 |
| y | 0 | 2 | 4 |
Now plotting all points obtained in the x y plane to draw a graph of both equations.

From the above graph we see that graphs of both lines intersect or meet at a point$\left( {2,2} \right)$.
Hence the solution of the given equation is$\left( {2,2} \right)$.
So, the correct answer is “{2,2} ”.
Note: While plotting deterrent points on x y plane if graph is not coming straight line then we can say that there is a mistake in calculations as we know that graph of linear equation is a straight line. Also, we can cross check graphs by putting points of intersection in given equations as points of intersection will satisfy both linear equations.
Recently Updated Pages
Master Class 8 Social Science: Engaging Questions & Answers for Success

Master Class 8 English: Engaging Questions & Answers for Success

Class 8 Question and Answer - Your Ultimate Solutions Guide

Master Class 8 Maths: Engaging Questions & Answers for Success

Master Class 8 Science: Engaging Questions & Answers for Success

Master Class 9 General Knowledge: Engaging Questions & Answers for Success

Trending doubts
What is BLO What is the full form of BLO class 8 social science CBSE

Citizens of India can vote at the age of A 18 years class 8 social science CBSE

Full form of STD, ISD and PCO

Advantages and disadvantages of science

Right to vote is a AFundamental Right BFundamental class 8 social science CBSE

What are the 12 elements of nature class 8 chemistry CBSE




