Question

Solve the following question:
How many tangents can a circle have?

Answer 1

Hint: For this question, we have to find the number of tangents in a circle. For that, we have to define the definition of the tangent and also for the circle. By using the definition to combine them, we will get the required result.

Complete step-by-step solution:
Considering the Euclidean plane geometry, a tangent can be defined as a line to a circle that touches the circle’s circumference at exactly one point but not entering the circle’s interior.

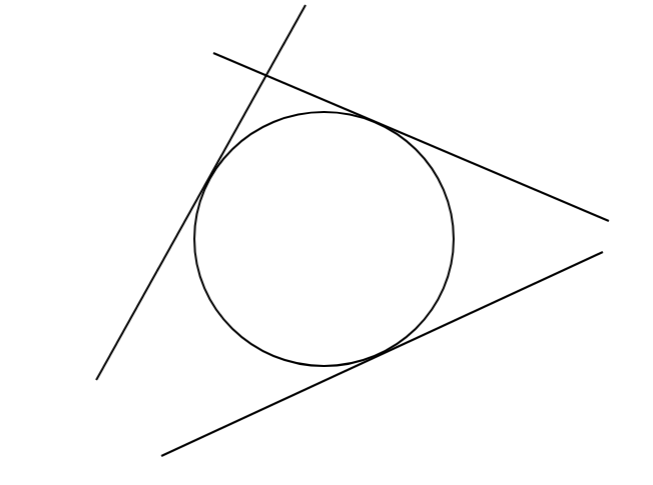
The above figure represents a circle with 3 tangents.
Since the circle is made up of infinite points, that is, infinite points come together in an array of a circle shape which forms a circle. Now, tangent being the line that touches a single point of a circle, we can draw infinite tangents, one from every point of the circle.

Therefore, a circle has infinite tangents.

Note: To find the equation of the tangent of a circle, we have to follow the steps as given below:
We first determine the equation of the circle given and bring it in terms of the standard equation of the circle. The standard equation of the circle is \[{\left( {x - a} \right)^2} + {\left( {y - b} \right)^2} = {r^2}\].
From the equation, we have to determine the coordinates of the centre of the circle. By comparing the given equation to the above standard equation of the circle, we can find the coordinates of the centre, that is, \[\left( {a,b} \right)\]
Now, we determine the slope or gradient of the radius which is given as \[m = \dfrac{{{y_2} - {y_1}}}{{{x_2} - {x_1}}}\].
According to the theorems of circles, the radius of the circle is perpendicular to the radius of the tangent. Considering the radius of the tangent as \[{m_t}\], we can find it by reciprocating the slope of the radius and reversing the sign. That implies, \[{m_t} = - \dfrac{1}{m}\]
Now by using the standard representation of the gradient-point equation of a straight line and substituting the slope of the tangent using the radius of the points as intercepts, we get the equation of the tangent as follows, with \[y\] as a subject.
\[ \Rightarrow y - {y_1} = m(x - {x_1})\]
Since the circle is a plane two-dimensional figure, it consists of combining infinite points, but the interior that is the area of the circle is finite which varies with the radius of the circle.