
Solve the following inequality:
${{\log }_{\dfrac{1}{3}}}(x-1)-{{\log }_{\dfrac{1}{3}}}(2x-3)<0$
Answer
596.7k+ views
Hint: We need to use the properties of logarithm first and then proceed to solve the given inequality. After that we have to find the domain of a given function with the conditions of logarithmic property and find the values of x for which function is defined.Then find the intersection values of x of inequality which gives a solution for inequality.
Complete step by step answer:
First we will use subtraction property of logarithm which is-
$\log m-\log n=\log \dfrac{m}{n}$
After applying the above property to the given inequality we get
${{\log }_{\dfrac{1}{3}}}\left( \dfrac{x-1}{2x-3} \right)<0..............(i)$
Now, first of all we need to look for the domain of logarithm. Domain of a function means the values of x for which the function is always defined. The basic definition of logarithm says
${{\log }_{a}}b=c\Rightarrow b={{a}^{c}}$ where $b>0,a>0$ & $a\ne 1$ .
Here our $b=\dfrac{x-1}{2x-3}$ and $a=\dfrac{1}{3}$which is already >0.
To make sure that our b is also greater than 0 we write,
$\dfrac{x-1}{2x-3}>0$
Now we need to solve this inequality and find the values of x for this inequality to hold.
From numerator we have, $x-1=0\Rightarrow x=1$ and from denominator we have, $2x-3=0\Rightarrow x=\dfrac{3}{2}$
Now $x=1$ and $x=\dfrac{3}{2}=1.5$ are our critical points which means that the sign of inequality changes at these points.
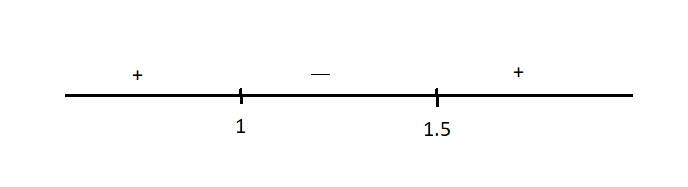
Here the + sign means that in that region the inequality holds and the – sign means that the sign of inequality changes means it does not hold for that region
Therefore, our x takes values in the + region $x\in (-\infty ,1)\cup (1.5,\infty ).............(ii)$ is our domain.
Now proceeding with equation (i) we have
${{\log }_{\dfrac{1}{3}}}\left( \dfrac{x-1}{2x-3} \right)<0$
Now we have to use the following results:
${{\log }_{a}}b>c\Rightarrow b>{{a}^{c}}$ whenever $a>1$ and
${{\log }_{a}}b>c\Rightarrow b<{{a}^{c}}$ whenever $a<1$
Using these results we have
$\left( \dfrac{x-1}{2x-3} \right)>{{\left( \dfrac{1}{3} \right)}^{0}}$
Since anything to the power 0 is equal to 1, we have
$\left( \dfrac{x-1}{2x-3} \right)>1$
Subtracting 1 on both sides, we have
$\left( \dfrac{x-1}{2x-3} \right)-1>0$
We take L.C.M and simplify further.
$\dfrac{x-1-(2x-3)}{2x-3}>0$
$\dfrac{-x+2}{2x-3}>0$
Multiplying both sides with -1 we have,
$\dfrac{x-2}{2x-3}<0$
Now we proceed as earlier.
From the numerator we have, $x-2=0\Rightarrow x=2$ .
From the denominator we have, $2x-3=0\Rightarrow x=\dfrac{3}{2}$ .
Now our critical points are $x=2$ and $x=\dfrac{3}{2}$ .
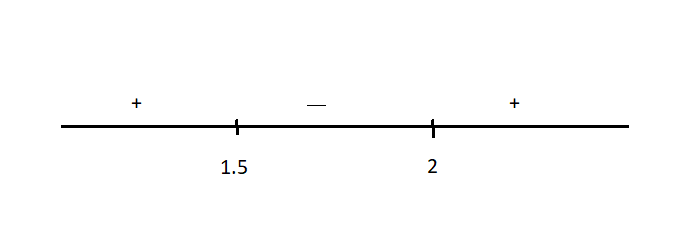
In this inequality the region with – sign will give us our result as our sign of inequality has reversed now. Therefore $x\in \left( \dfrac{3}{2},2 \right)..............(iii)$
Now we need to check if these values are in our domain or not and if not we will eliminate those values of x. For this we need to find the intersection of values of x in (ii) and (iii):
$\left( (-\infty ,1)\cup \left( \dfrac{3}{2},\infty \right) \right)\cap \left( \dfrac{3}{2},2 \right)$, which gives
$x\in \left( \dfrac{3}{2},2 \right)$
Hence, our answer is $x\in \left( \dfrac{3}{2},2 \right)$.
Note: (a). We should always remember to change signs whenever multiplying an inequality with a negative number on both sides.
(b). We should never forget to check the domain of a function first and then proceed with the given problem. The coefficient of x must be positive when proceeding to find the critical points.
(c). Also when drawing the number line the region on the rightmost must be positive.
One thing to notice here is, for domain we had, $\left( \dfrac{x-1}{2x-3} \right)>0$ and when we had proceeded further we had $\left( \dfrac{x-1}{2x-3} \right)>1$ and then we had taken the intersection of the following two inequalities. We can see that the expression on the L.H.S of both the inequalities is the same and the first inequality says that the expression is greater than 0 and the second one says that the expression is greater than 1 and taking intersection basically means that the condition of both must be satisfied. So, intuitively we could have skipped this step as something which is greater than 1 is also greater than 0.
Complete step by step answer:
First we will use subtraction property of logarithm which is-
$\log m-\log n=\log \dfrac{m}{n}$
After applying the above property to the given inequality we get
${{\log }_{\dfrac{1}{3}}}\left( \dfrac{x-1}{2x-3} \right)<0..............(i)$
Now, first of all we need to look for the domain of logarithm. Domain of a function means the values of x for which the function is always defined. The basic definition of logarithm says
${{\log }_{a}}b=c\Rightarrow b={{a}^{c}}$ where $b>0,a>0$ & $a\ne 1$ .
Here our $b=\dfrac{x-1}{2x-3}$ and $a=\dfrac{1}{3}$which is already >0.
To make sure that our b is also greater than 0 we write,
$\dfrac{x-1}{2x-3}>0$
Now we need to solve this inequality and find the values of x for this inequality to hold.
From numerator we have, $x-1=0\Rightarrow x=1$ and from denominator we have, $2x-3=0\Rightarrow x=\dfrac{3}{2}$
Now $x=1$ and $x=\dfrac{3}{2}=1.5$ are our critical points which means that the sign of inequality changes at these points.
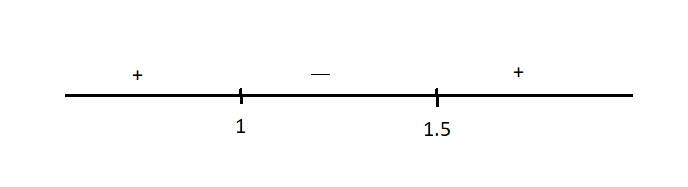
Here the + sign means that in that region the inequality holds and the – sign means that the sign of inequality changes means it does not hold for that region
Therefore, our x takes values in the + region $x\in (-\infty ,1)\cup (1.5,\infty ).............(ii)$ is our domain.
Now proceeding with equation (i) we have
${{\log }_{\dfrac{1}{3}}}\left( \dfrac{x-1}{2x-3} \right)<0$
Now we have to use the following results:
${{\log }_{a}}b>c\Rightarrow b>{{a}^{c}}$ whenever $a>1$ and
${{\log }_{a}}b>c\Rightarrow b<{{a}^{c}}$ whenever $a<1$
Using these results we have
$\left( \dfrac{x-1}{2x-3} \right)>{{\left( \dfrac{1}{3} \right)}^{0}}$
Since anything to the power 0 is equal to 1, we have
$\left( \dfrac{x-1}{2x-3} \right)>1$
Subtracting 1 on both sides, we have
$\left( \dfrac{x-1}{2x-3} \right)-1>0$
We take L.C.M and simplify further.
$\dfrac{x-1-(2x-3)}{2x-3}>0$
$\dfrac{-x+2}{2x-3}>0$
Multiplying both sides with -1 we have,
$\dfrac{x-2}{2x-3}<0$
Now we proceed as earlier.
From the numerator we have, $x-2=0\Rightarrow x=2$ .
From the denominator we have, $2x-3=0\Rightarrow x=\dfrac{3}{2}$ .
Now our critical points are $x=2$ and $x=\dfrac{3}{2}$ .
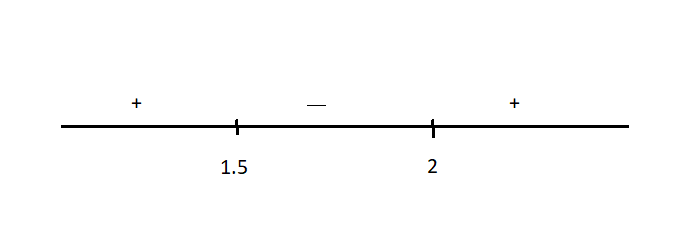
In this inequality the region with – sign will give us our result as our sign of inequality has reversed now. Therefore $x\in \left( \dfrac{3}{2},2 \right)..............(iii)$
Now we need to check if these values are in our domain or not and if not we will eliminate those values of x. For this we need to find the intersection of values of x in (ii) and (iii):
$\left( (-\infty ,1)\cup \left( \dfrac{3}{2},\infty \right) \right)\cap \left( \dfrac{3}{2},2 \right)$, which gives
$x\in \left( \dfrac{3}{2},2 \right)$
Hence, our answer is $x\in \left( \dfrac{3}{2},2 \right)$.
Note: (a). We should always remember to change signs whenever multiplying an inequality with a negative number on both sides.
(b). We should never forget to check the domain of a function first and then proceed with the given problem. The coefficient of x must be positive when proceeding to find the critical points.
(c). Also when drawing the number line the region on the rightmost must be positive.
One thing to notice here is, for domain we had, $\left( \dfrac{x-1}{2x-3} \right)>0$ and when we had proceeded further we had $\left( \dfrac{x-1}{2x-3} \right)>1$ and then we had taken the intersection of the following two inequalities. We can see that the expression on the L.H.S of both the inequalities is the same and the first inequality says that the expression is greater than 0 and the second one says that the expression is greater than 1 and taking intersection basically means that the condition of both must be satisfied. So, intuitively we could have skipped this step as something which is greater than 1 is also greater than 0.
Recently Updated Pages
Master Class 12 Social Science: Engaging Questions & Answers for Success

Master Class 12 Physics: Engaging Questions & Answers for Success

Master Class 12 Maths: Engaging Questions & Answers for Success

Master Class 12 Economics: Engaging Questions & Answers for Success

Master Class 12 Chemistry: Engaging Questions & Answers for Success

Master Class 12 Business Studies: Engaging Questions & Answers for Success

Trending doubts
What are the major means of transport Explain each class 12 social science CBSE

Which are the Top 10 Largest Countries of the World?

Draw a labelled sketch of the human eye class 12 physics CBSE

How much time does it take to bleed after eating p class 12 biology CBSE

Explain sex determination in humans with line diag class 12 biology CBSE

Plot a graph between potential difference V and current class 12 physics CBSE




