Question

Solve the equations $7x-15y=2$ and $x+2y=3$ by using the substitution method.

Answer 1

Hint: In this problem we need to solve the given system of linear equations by using the substitution method. In this method we will first consider any one of the equations and calculate the value of one variable in terms of another variable by using some basic mathematical operation. After that we will substitute the calculated value in the other given equation and convert that equation in terms of only a single variable. Now we can perform some mathematical operations and simplify the equation to get the value of one variable. After having the value of one variable we will substitute that value in any one of the given equations and calculate the value of another variable.

Complete step by step solution:
Given equations are $7x-15y=2$ and $x+2y=3$.
Considering the equation $x+2y=3$.
From the above equation we can get the value of $x$ by subtracting $2y$ from both sides of the above equation, then we will have
$x=3-2y$
Substituting the above calculated value in the another given equation $7x-15y=2$, then we will have
$7\left( 3-2y \right)-15y=2$
Applying distribution law of multiplication over subtraction in the above equation, then we will get
$\begin{align}
  & 7\times 3-7\times 2y-15y=2 \\
 & \Rightarrow 21-14y-15y=2 \\
 & \Rightarrow 21-29y=2 \\
\end{align}$
Subtracting the value $21$ from both sides of the above equation, then the above equation is modified as
$\begin{align}
  & 21-29y-21=2-21 \\
 & \Rightarrow -29y=-19 \\
\end{align}$
Dividing the above equation with $-29$ on both sides, then we will have
$\therefore y=\dfrac{19}{29}$
Substituting the above calculated $y$ value in the equation $x=3-2y$ and simplifying the equation, then we will get
$\begin{align}
  & x=3-2\left( \dfrac{19}{29} \right) \\
 & \Rightarrow x=\dfrac{3\times 29-2\times 19}{29} \\
 & \Rightarrow x=\dfrac{87-38}{29} \\
 & \therefore x=\dfrac{49}{29} \\
\end{align}$

Hence the solution of the given equations $7x-15y=2$ and $x+2y=3$ is $x=\dfrac{49}{29}$, $y=\dfrac{19}{29}$.
We can also observe the graph of the given equations as given below

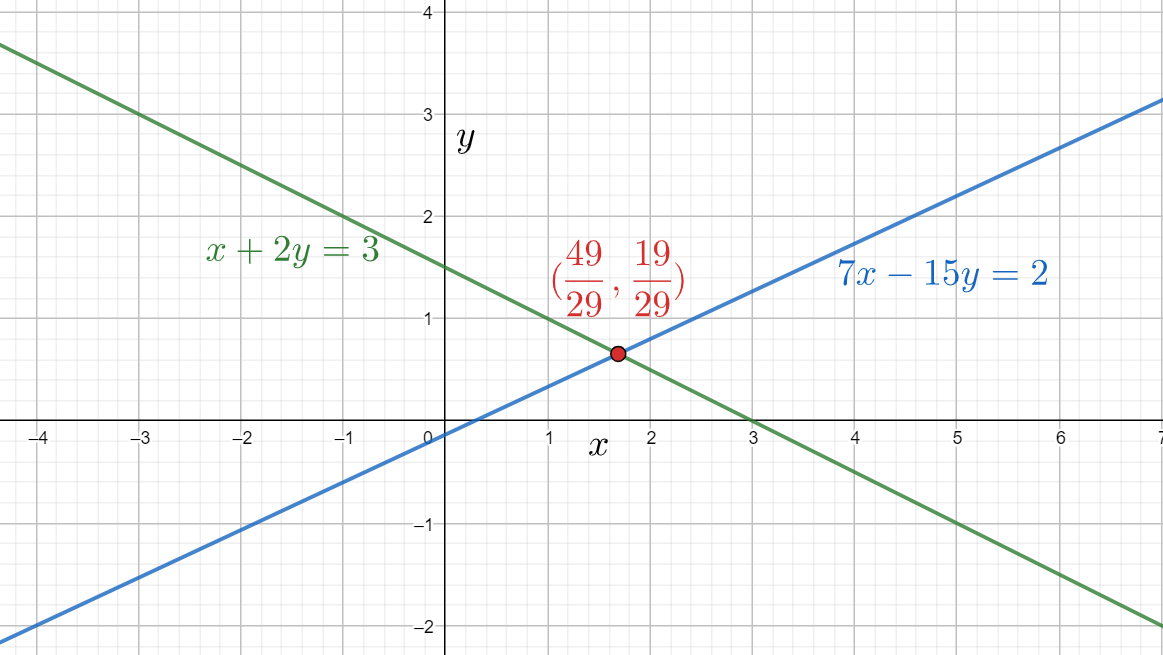
Note: For this problem we have considered the equation $x+2y=3$ and calculated the value of $x$ from it. Instead of this we can also calculate the value of the same $x$ from $7x-15y=2$ or calculate the value of $y$ from any one of the both given equations. But it will take some time to simplify the equations since we will get the values in fractions. So I didn't follow that procedure.