Question

How do you solve the equations $2x+3y=2$ and $x+6y=4$?

Answer 1

Hint: Now we are given with two linear equations. To find the solution we will graph the two equations. Now to graph the equation of line express one variable in terms of another. Let us say we have expressed x in terms of y. then we substitute different values of x and find the corresponding values of y. hence we get the points (x, y) on the line. Now plot the points and draw a line passing through both the points. Hence we get two lines. Now the intersection of the two lines is the solution of the given equation.

Complete step by step solution:
Now the given equations are linear equations in two variables.
We know that linear equations in two variables are lines in the XY plane. Hence each given equation represents a line in the XY plane.
Now we want to find the solution of the equation. Hence we want to find the point (x, y) which lies on both sides of the equation. Hence we want to find the intersection point of the two lines.
Now let us plot the two lines on a graph.
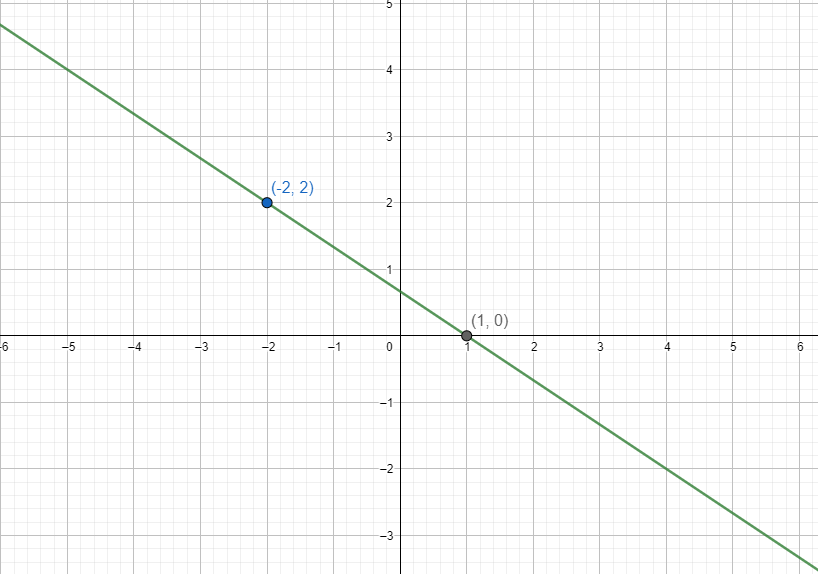
Consider the equation $2x+3y=2$
Now on rearranging the terms of the equation we get,
$\begin{align}
  & \Rightarrow 2x=2-3y \\
 & \Rightarrow x=1-\dfrac{3}{2}y \\
\end{align}$
Now let us find the points satisfying the equation.
On substituting y = 0 in the above equation we get x = 1.
Similarly on substituting y = 2 in the above equation we get x = - 2.
Hence we have the points (1, 0) and the points (-2, 2) are the points on line.
Now we will plot the points and draw a graph passing through both the points.
Hence we get,

Now consider the equation $x+6y=4$
On rearranging the terms on the equation we get $x=4-6y$
Now let us substitute y = 0, hence we get x = 4.
Similarly on substituting y = 1 we get x = -2.
Hence (4, 0) and (-2, 1) are the points on the line. Hence we will plot the lines and draw the graph of the line and find the point of intersection with the previous line hence we get,

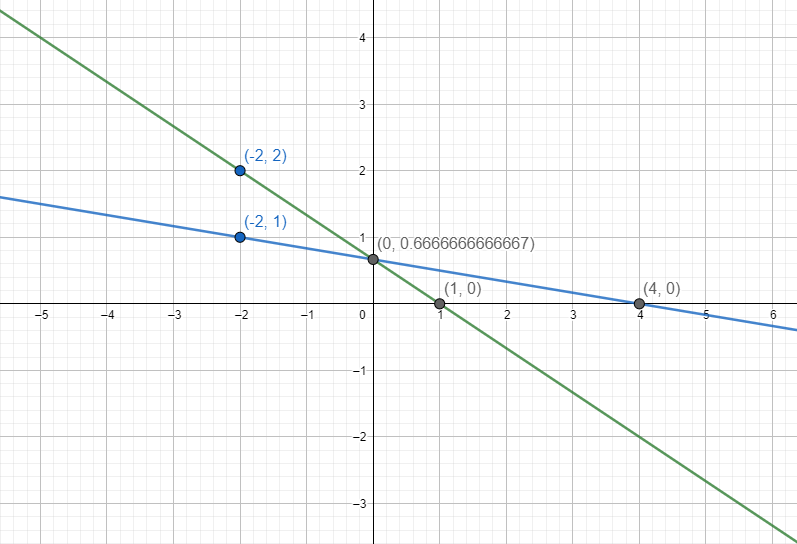
Hence the point of intersection of the graph is (0, 0.666)
Hence the solution of the graphs is x = 0 and y = 0.666….

Note: Now note that two lines may intersect or may not intersect. If the lines are parallel then the lines do not intersect and we have no solution in this case. Similarly if the lines are coincident then there are infinite solutions.