Question

Show that the opposite sides in a regular hexagon are parallel to each other?

Answer 1

Hint: We start solving the problem by drawing two diagonals for the points that are adjacent to each other. We find the angles at each point of the structure formed by the diagonals and actual sides of the hexagon by using angle in a regular hexagon is equal. On finding the angles of the figure, we get the required proof.

Complete step-by-step answer:
Given that we have a regular hexagon and we need to prove that the opposite sides of a given regular hexagon are parallel to each other.
Let us draw the figure of a regular hexagon ABCDEF as shown below.

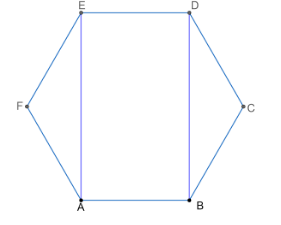
If we prove side AB is parallel to the side DE, then we can say that the remaining opposite sides are also parallel to each other.
We start solving the problem by drawing the diagonals AE and BD.
We know that any angle in a given regular hexagon is $ {{120}^{o}} $ , and all the sides are equal in a regular hexagon.
From triangle AEF, we get FA=EF, as they are the sides of the hexagon. We know that in a triangle angles opposite to the equal sides are equal.
So, we get $ \angle FAE=\angle AEF $ .
We know that the sum of all angles in triangle AEF is $ {{180}^{o}} $ .
So, we have got $ \angle EFA+\angle FAE+\angle AEF={{180}^{o}} $ .
Here $ \angle EFA={{120}^{o}} $ , as each angle in a regular hexagon is $ {{120}^{o}} $ .
So, we have got $ {{120}^{o}}+\angle FAE+\angle FAE={{180}^{o}} $ .
We have got $ 2\angle FAE={{180}^{o}}-{{120}^{o}} $ .
We have got $ 2\angle FAE={{60}^{o}} $ .
We have got $ \angle FAE=\dfrac{{{60}^{o}}}{2} $ .
We have got $ \angle FAE={{30}^{o}} $ .
So, we have got $ \angle FAE=\angle AEF={{30}^{o}} $ .
We have got $ \angle FAE+\angle EFB={{120}^{o}} $ , as it represents angle A in the hexagon.
We have got $ {{30}^{0}}+\angle EFB={{120}^{o}} $ .
We have got $ \angle EFB={{120}^{o}}-{{30}^{o}} $ .
We have got $ \angle EFB={{90}^{o}} $ ---(1).
We have got $ \angle AEF+\angle AED={{120}^{o}} $ , as it represents angle E in the hexagon.
We have got $ {{30}^{0}}+\angle AED={{120}^{o}} $ .
We have got $ \angle AED={{120}^{o}}-{{30}^{o}} $ .
We have got $ \angle AED={{90}^{o}} $ ---(2).
From triangle BCD, we get BC=CD, as they are the sides of the hexagon. We know that in a triangle angles opposite to the equal sides are equal.
So, we get $ \angle CDB=\angle DBC $ .
We know that the sum of all angles in triangle BCD is $ {{180}^{o}} $ .
So, we have got $ \angle BCD+\angle CDB+\angle DBC={{180}^{o}} $ .
Here $ \angle BCD={{120}^{o}} $ , as each angle in a regular hexagon is $ {{120}^{o}} $ .
So, we have got $ {{120}^{o}}+\angle CDB+\angle DBC={{180}^{o}} $ .
We have got $ 2\angle CDB={{180}^{o}}-{{120}^{o}} $ .
We have got $ 2\angle CDB={{60}^{o}} $ .
We have got $ \angle CDB=\dfrac{{{60}^{o}}}{2} $ .
We have got $ \angle CDB={{30}^{o}} $ .
So, we have got $ \angle CDB=\angle DBC={{30}^{o}} $ .
We have got $ \angle CDB+\angle BDE={{120}^{o}} $ , as it represents angle D in the hexagon.
We have got $ {{30}^{0}}+\angle BDE={{120}^{o}} $ .
We have got $ \angle BDE={{120}^{o}}-{{30}^{o}} $ .
We have got $ \angle BDE={{90}^{o}} $ ---(3).
We have got $ \angle DBC+\angle DBA={{120}^{o}} $ , as it represents angle E in the hexagon.
We have got $ {{30}^{0}}+\angle DBA={{120}^{o}} $ .
We have got $ \angle DBA={{120}^{o}}-{{30}^{o}} $ .
We have got $ \angle DBA={{90}^{o}} $ ---(4).
From equations (1), (2), (3) and (4), we get all the angles present in ABDE are right angles. So, ABDE forms a rectangle. We know that the opposite sides are parallel to each other in a rectangle.
So, we get AB is parallel to DE. Similarly, we can prove for other sides also.
∴ We have proved that the opposite sides are parallel to each other in a regular hexagon.

Note: We should remember that all sides are equal in a regular polygon of any sides. We also used the fact that if two lines are perpendicular to the same line, then those two lines are parallel to each other. We should take appropriate sides and angles to prove this type of problem.