Question

Show that the cyclic trapezium is isosceles.

Answer 1

Hint: In order to prove the trapezium to be isosceles first draw the figure of cyclic trapezium, expand the figure in order to draw it as a parallelogram. Use the property of cyclic trapezium as well as parallelogram to prove the answer.

Complete step-by-step solution -
We will use the following figure in order to solve the problem.

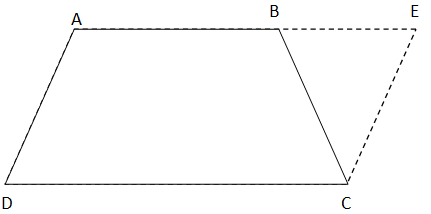
Let ABCD be the cyclic trapezium with $AB||CD$ .
Through C let us draw CE parallel to AD meeting AB at E.
So,
AECD is a parallelogram
So, for parallelogram AECD
$\angle D = \angle AEC$ as opposite angles of a parallelogram are equal..........(i)
But,
$\angle D + \angle ABC = {180^0}$ as opposite angles of a cyclic quadrilateral are supplementary.............(ii)
So, from (i) and (ii) we have
$\angle AEC + \angle ABC = {180^0}$
But,
$\angle AEC + \angle CEB = {180^0}$ due to linear pair
So,
$\angle ABC = \angle CEB$ …………….(iii)
So,
$CE = CB$ as sides opposite equal angles are equal…………….(iv)
But,
$CE = AD$ as they are opposite sides of parallelogram AECD.
So from (iv) we get,
$AD = CB$
Hence, cyclic trapezium ABCD is isosceles as the opposite sides which are not parallel are equal.

Note: A cyclic quadrilateral or inscribed quadrilateral is a quadrilateral whose vertices all lie on a single circle. This circle is called the circumcircle or circumscribed circle, and the vertices are said to be concyclic. Students must draw the figure to solve such types of problems and must remember the properties of cyclic quadrilaterals.