
Show graphically, the binding energy per nucleon with the mass number and also explain how energy is released in the process of nuclear fission and nuclear fusion.
Answer
511.8k+ views
Hint:Initially, we will discuss the basic idea behind binding energy. Then, gradually we will discuss the stability of an atom with binding energy as a reference. Then we will discuss nuclear fusion and nuclear fission.
Complete answer:
Firstly, let us define binding energy. It can be simply defined as the amount of energy required to break a nucleus into its constituents. In simple words, it can be defined as the breaking energy needed to break a nucleus into individual neutrons and protons.
Let us take some examples; the binding energy for oxygen (${O^{16}}$) atom, where $16$ is the mass number or the atomic mass of oxygen in $amu$ is approximately $128{\text{ }}MeV$. This suggests that $128{\text{ }}MeV$ amount of energy is required to break the oxygen nucleus into individual neutrons and protons. In other, if we want to separate all the $16$ protons and neutrons in the nucleus apart, energy of $128{\text{ }}MeV$ should be supplied to the atom or basically to the nucleus.
Similarly, the binding energy for Uranium (${U^{235}}$) atom, where $235$ is the mass number or the atomic mass of uranium in ${\text{amu}}$ is approximately $1786{\text{ }}MeV$. This suggests that $1786{\text{ }}MeV$ amount of energy is required to break the uranium nucleus into individual neutrons and protons. In other, if we want to separate all the $235$ protons and neutrons in the nucleus apart, energy of $1786{\text{ }}MeV$ should be supplied to the atom or basically to the nucleus.
Now, if we compare the binding energies of the two atoms, then, can we say that ${U^{235}}$ nucleus is more stable than ${O^{16}}$ nucleus as it needs more energy to break apart? The answer will be no. This is because uranium has $235$ neutrons and protons to separate whereas oxygen has only $16$. Thus, these two values cannot be compared to conclude for stability of the atoms.
Thus, we use the concept of binding energy per nucleon. This is a more comparable parameter as we are comparing energy required by each nucleon (neutron or proton) to get separated. For a nucleus, the value can be calculated as
$\text{Binding Energy per Nucleon} = \dfrac{\text{Binding Energy}}{\text{Number of nucleons}} \\ $
Thus, substituting the values for ${O^{16}}$, we get
$\text{Binding Energy per Nucleon} \approx 8{\text{ }}MeV \\ $
And for ${U^{235}}$, we get
\[\text{Binding Energy per Nucleon} \approx 7.6{\text{ }}MeV \\ \]
Thus, it is apparent that ${O^{16}}$ nucleus is more stable than ${U^{235}}$ as an individual nucleon of ${O^{16}}$ requires more energy to separate from the nucleus than that of a nucleon in ${U^{235}}$ nucleus.
Now, the graph of binding energy per nucleon with the mass number turns out to be something like
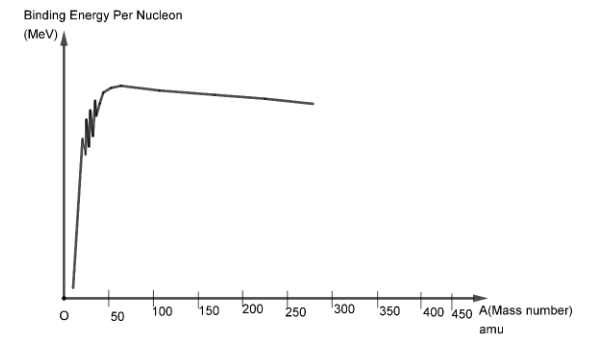
Here, we can see that the binding energy per nucleon initially increases with mass number.Then it reaches a peak value near $56{\text{ }}amu$ and then gradually starts decreasing, but the decrease is very slight. It nearly remains the same after the peak value.If we observe, then we see that the peak binding energy is attained at $56{\text{ }}amu$ which refers to the iron ($F{e^{56}}$) nucleus. This means that \[F{e^{56}}\] is the most stable nucleus available.
Now, let us discuss the energy released in nuclear fission and nuclear fusion. Nuclear fission is the process in which a heavy nucleus is split into two lighter nuclei (daughter nuclei).Whereas, nuclear fusion is the process in which two light nuclei are combined to form a heavier nucleus. In both cases the mass of the products is slightly less than mass of the initial nuclei. This mass difference is released as energy.
For example, when ${U^{235}}$ nucleus is bombarded with a neutron, it splits into two daughter nuclei as Krypton ($K{r^{92}}$) and Barium ($B{a^{141}}$). If we observe, the mass of the products is \[92 + 141 = 233\]. Whereas, the mass of the original nucleus was $235$.Thus, the mass of the products is less than the mass of the initial nucleus. This mass difference is released as energy during the fission.
Similarly, when deuterium (${D^2}$) and tritium (${T^3}$) undergo nuclear fusion, it forms a helium ($H{e^4}$) nucleus and a neutron. Thus, clearly here also the mass of the products is ${\text{4}}$ whereas the mass of the initial nuclei was ${\text{2 + 3 = 5}}$. Thus, the mass of the products is less than the mass of the initial nuclei. Thus, this mass difference is released as energy during the fusion process.
Note:Students often get confused intuitively with the literary sense of the name binding energy as the energy required to bind the nucleons together. But the actual sense is the amount of energy required to break the binding between the nucleons. Students also commit errors thinking that energy has to be supplied for nuclear fission so no energy is released while a fission process is taking place. But in actuality, the nucleus is bombarded with a neutron for triggering the fission to take place. The neutron released after the fusion has a minimal mass so it is playing a very minor role in affecting the energy released during the fusion process.
Complete answer:
Firstly, let us define binding energy. It can be simply defined as the amount of energy required to break a nucleus into its constituents. In simple words, it can be defined as the breaking energy needed to break a nucleus into individual neutrons and protons.
Let us take some examples; the binding energy for oxygen (${O^{16}}$) atom, where $16$ is the mass number or the atomic mass of oxygen in $amu$ is approximately $128{\text{ }}MeV$. This suggests that $128{\text{ }}MeV$ amount of energy is required to break the oxygen nucleus into individual neutrons and protons. In other, if we want to separate all the $16$ protons and neutrons in the nucleus apart, energy of $128{\text{ }}MeV$ should be supplied to the atom or basically to the nucleus.
Similarly, the binding energy for Uranium (${U^{235}}$) atom, where $235$ is the mass number or the atomic mass of uranium in ${\text{amu}}$ is approximately $1786{\text{ }}MeV$. This suggests that $1786{\text{ }}MeV$ amount of energy is required to break the uranium nucleus into individual neutrons and protons. In other, if we want to separate all the $235$ protons and neutrons in the nucleus apart, energy of $1786{\text{ }}MeV$ should be supplied to the atom or basically to the nucleus.
Now, if we compare the binding energies of the two atoms, then, can we say that ${U^{235}}$ nucleus is more stable than ${O^{16}}$ nucleus as it needs more energy to break apart? The answer will be no. This is because uranium has $235$ neutrons and protons to separate whereas oxygen has only $16$. Thus, these two values cannot be compared to conclude for stability of the atoms.
Thus, we use the concept of binding energy per nucleon. This is a more comparable parameter as we are comparing energy required by each nucleon (neutron or proton) to get separated. For a nucleus, the value can be calculated as
$\text{Binding Energy per Nucleon} = \dfrac{\text{Binding Energy}}{\text{Number of nucleons}} \\ $
Thus, substituting the values for ${O^{16}}$, we get
$\text{Binding Energy per Nucleon} \approx 8{\text{ }}MeV \\ $
And for ${U^{235}}$, we get
\[\text{Binding Energy per Nucleon} \approx 7.6{\text{ }}MeV \\ \]
Thus, it is apparent that ${O^{16}}$ nucleus is more stable than ${U^{235}}$ as an individual nucleon of ${O^{16}}$ requires more energy to separate from the nucleus than that of a nucleon in ${U^{235}}$ nucleus.
Now, the graph of binding energy per nucleon with the mass number turns out to be something like

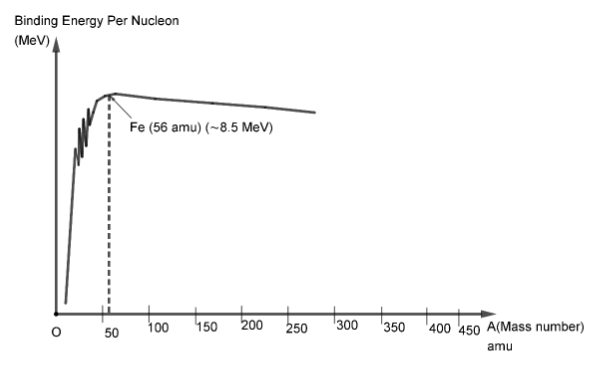
Here, we can see that the binding energy per nucleon initially increases with mass number.Then it reaches a peak value near $56{\text{ }}amu$ and then gradually starts decreasing, but the decrease is very slight. It nearly remains the same after the peak value.If we observe, then we see that the peak binding energy is attained at $56{\text{ }}amu$ which refers to the iron ($F{e^{56}}$) nucleus. This means that \[F{e^{56}}\] is the most stable nucleus available.

Now, let us discuss the energy released in nuclear fission and nuclear fusion. Nuclear fission is the process in which a heavy nucleus is split into two lighter nuclei (daughter nuclei).Whereas, nuclear fusion is the process in which two light nuclei are combined to form a heavier nucleus. In both cases the mass of the products is slightly less than mass of the initial nuclei. This mass difference is released as energy.
For example, when ${U^{235}}$ nucleus is bombarded with a neutron, it splits into two daughter nuclei as Krypton ($K{r^{92}}$) and Barium ($B{a^{141}}$). If we observe, the mass of the products is \[92 + 141 = 233\]. Whereas, the mass of the original nucleus was $235$.Thus, the mass of the products is less than the mass of the initial nucleus. This mass difference is released as energy during the fission.
Similarly, when deuterium (${D^2}$) and tritium (${T^3}$) undergo nuclear fusion, it forms a helium ($H{e^4}$) nucleus and a neutron. Thus, clearly here also the mass of the products is ${\text{4}}$ whereas the mass of the initial nuclei was ${\text{2 + 3 = 5}}$. Thus, the mass of the products is less than the mass of the initial nuclei. Thus, this mass difference is released as energy during the fusion process.
Note:Students often get confused intuitively with the literary sense of the name binding energy as the energy required to bind the nucleons together. But the actual sense is the amount of energy required to break the binding between the nucleons. Students also commit errors thinking that energy has to be supplied for nuclear fission so no energy is released while a fission process is taking place. But in actuality, the nucleus is bombarded with a neutron for triggering the fission to take place. The neutron released after the fusion has a minimal mass so it is playing a very minor role in affecting the energy released during the fusion process.
Recently Updated Pages
Master Class 12 Economics: Engaging Questions & Answers for Success

Master Class 12 Physics: Engaging Questions & Answers for Success

Master Class 12 English: Engaging Questions & Answers for Success

Master Class 12 Social Science: Engaging Questions & Answers for Success

Master Class 12 Maths: Engaging Questions & Answers for Success

Master Class 12 Business Studies: Engaging Questions & Answers for Success

Trending doubts
Which are the Top 10 Largest Countries of the World?

What are the major means of transport Explain each class 12 social science CBSE

Draw a labelled sketch of the human eye class 12 physics CBSE

Why cannot DNA pass through cell membranes class 12 biology CBSE

Differentiate between insitu conservation and exsitu class 12 biology CBSE

Draw a neat and well labeled diagram of TS of ovary class 12 biology CBSE




