Question

Select the correct option to complete the statement: ‘Two parallel lines have: ’
(a) a common point
(b) two common points
(c) no common point
(d) infinite common points

Answer 1

Hint: Understand the definitions of different types of lines such as parallel lines, intersecting lines and coincident lines. Observe their general equations and properties to determine the correct option.

Complete step by step answer:
Here, we have been provided with four options and we have to determine the correct one to complete the statement: - ‘Two parallel lines have: ‘. First, let us see the following different types of lines.
1. Intersecting lines: -
Two lines are called intersecting lines when they meet or cut each other at a particular point. The general equation of two intersecting lines can be given as: -
\[\Rightarrow {{a}_{1}}x+{{b}_{1}}y+{{c}_{1}}=0\] - (1)
\[\Rightarrow {{a}_{2}}x+{{b}_{2}}y+{{c}_{2}}=0\] - (2)
The figure shown below represents two intersecting lines.

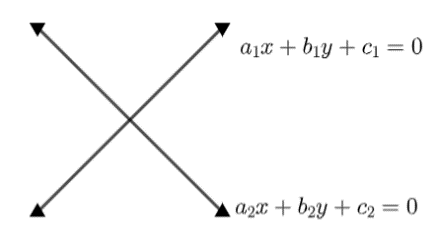
Clearly, we can see that two intersecting lines have only one point in common.
2. Parallel lines: -
Two lines are called parallel lines of the distance between them remains constant throughout their extension in the infinite plane. The general equation of two parallel lines can be given as: -
\[\Rightarrow {{a}_{1}}x+{{b}_{1}}y+{{c}_{1}}=0\] - (1)
\[\Rightarrow {{a}_{2}}x+{{b}_{2}}y+{{c}_{2}}=0\] - (2)
The constant distance between these lines is \[\left| {{c}_{1}}-{{c}_{2}} \right|\]. Clearly, we can see that the slope of both the lines are equal. So, in general parallel lines have the same slope. The figure shown below represents two parallel lines.

Clearly, we can see that two parallel lines have no point in common.
3. Coincident lines: -
Two lines are called coincident lines if they overlap with each other. The general equation of two coincident lines can be given as: -
\[\Rightarrow ax+by+c=0\] - (1)
\[\Rightarrow k\left( ax+by+c \right)=0\] - (2)
Here, k is any constant.
The figure shown below represents two coincident lines: -

Clearly, we can see that two coincident lines have infinite common points.
Therefore, on reading the above three types of lines we come to the conclusion that ‘two parallel lines have no common point’.

So, the correct answer is “Option c”.

Note: One may note that to solve the above question we must know the definitions of different types of lines. Here, we have used their differences in properties as our main points. You must know the general equations of such types of lines so that in case you forget the definitions, these equations will help you to solve the problem.