Question

What is the resistance of the voltmeter shown in the circuit?

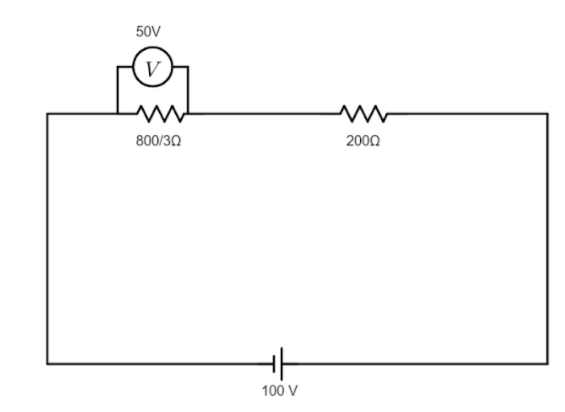
A. $\dfrac{{800}}{3}\Omega $
B. $800\,\Omega $
C. $1000\,\Omega $
D. $200\,\Omega $

Answer 1

Hint: In a series connection, the current is each element is equal to the supply current
$I = {I_1} = {I_2}.......$ whereas the supply voltage is equal to the sum of individual voltages
$V = {V_1} + {V_2}.......$
Ohm’s law states that for given physical conditions, the voltage drop across a particular element in a circuit is directly proportional to the current flowing through the element.
The mathematical expression is given as $V \propto I$
Replacing the proportionality sign we get $V = IR$ where R is the resistance of the element.

Complete step by step solution:
Since the voltmeter is connected in parallel across the $\dfrac{{800}}{3}\Omega $, the voltage drop across the $\dfrac{{800}}{3}\Omega $ resistor is $50\,V$ .
We know that in a series connection the voltage is the sum of voltage drops across each element.
Hence, $100 = {V_{200\Omega }} + {V_{\dfrac{{800}}{3}\Omega }}$
$ \Rightarrow {V_{200\Omega }} = 50V$ .
Now the current flowing through the $200\,\Omega $ is $I = \dfrac{V}{R}$ (by ohm’s law)
$ \Rightarrow I = \dfrac{{50}}{{200}}$
$ \Rightarrow I = \dfrac{1}{4}A$
In a series connection the current flowing through each element is the same.
Hence, ${I_{(\dfrac{{800}}{3}\Omega + 50V)}} = \dfrac{1}{4}A$ where $\dfrac{{800}}{3}\Omega + 50V$ represents the parallel connection of the $50\,V$voltmeter and the $\dfrac{{800}}{3}\Omega $ resistance.
The equivalent resistance of the connection( $50\,V$voltmeter and the $\dfrac{{800}}{3}\Omega $ resistance) is given as
$R = \dfrac{V}{I}$ using ohm’s law
$ \Rightarrow R = \dfrac{{50}}{{\dfrac{1}{4}}}$
$ \Rightarrow R = 200\Omega $
So, the equivalent resistance of the $\dfrac{{800}}{3}\Omega + 50V$ combination is $R = 200\Omega $ .
Let the resistance of the voltmeter be ${R_V}$.
The parallel equivalent is given by $R = \dfrac{{{R_V} \times \dfrac{{800}}{3}}}{{{R_V} + \dfrac{{800}}{3}}}$
We have calculated the value of parallel equivalent to be $R = 200\Omega $
Substituting in the equation
$200 = \dfrac{{{R_V} \times \dfrac{{800}}{3}}}{{{R_V} + \dfrac{{800}}{3}}}$
Further solving this
$ \Rightarrow 200 = \dfrac{{800{R_V}}}{{3{R_V} + 800}}$
$ \Rightarrow 600{R_V} + 160000 = 800{R_V}$
$ \Rightarrow {R_V} = 800\Omega $
Hence option B is correct.

Note: Voltmeters are devices with high resistances to allow least possible current to flow and are always connected in parallel to prevent heating of the circuit. Simplifying the circuit into smaller equivalents and then backward substituting the values is better than introducing new circuit variables for every branch in the circuit since it prevents the situation of handling multiple equations at the same time.