Question

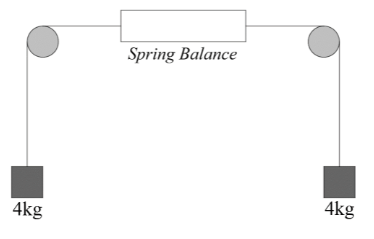
What is the reading shown in the spring balance?

Answer 1

Hint: Spring balance simply measures the weight on its spring. In the above figure there are two masses attached with a string to two respective pulleys and then to a spring balance. There are two forces which are working on each block, one is the force exerted by gravity and another is the tension of rope which is pulling the mass in upward direction.

Complete step by step answer:
Force is equal to the multiplication of mass and acceleration. Weight is a force exerted on a body due to gravity. The acceleration due to gravity is g which is equal to $9.8\,m/{{s}^{2}}$.Let us consider the first system of spring balance.On the first mass pulley system, the force due to the tension in rope is equal to $T-4g=4a$, where $g$ is the acceleration due to gravity and $a$ is the acceleration of the object.

What we have done here is that we have added up all the forces working on the object, since they were in opposite directions, hence the negative sign has occurred, and then the total force has been put equal to mass multiplied by acceleration, mass was 4Kg and acceleration is assumed to be ‘$a$’. Now because both the masses are equal on both sides, the system will stay in rest, hence the acceleration ‘$a$’ becomes zero. So,
$T-4g=0$
$\Rightarrow T=4g=40\,Kgm{{s}^{2}}$
There are two ropes which are pulling the spring in the opposite directions, the total force applied on the spring system will be the sum of those two tensions:
$F=T+T \\
\Rightarrow F=2T \\
\Rightarrow F=2\times 40 \\
\therefore F=80\,Kgm{{s}^{-2}}$

Hence the reading shown on spring balance will be 80 N.

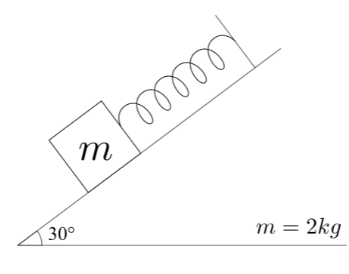
Now, let us consider the second spring balance system.The forces acting on the block are the gravitational forces that act vertically downward and the tension in the spring that acts against the stretching of the spring. Let us consider the inclined plane as the reference for the forces acting on the block. Hence, as we have taken an inclined reference, we have to consider the components of the gravitational force. The forces acting on the block can be shown as in the figure,

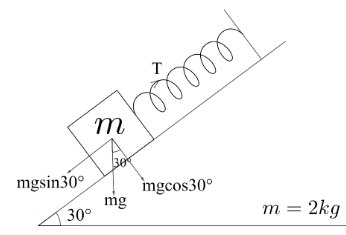
Due to the restoring force, the tensional force will be in the upwards direction on the block. The component of the gravitational force in the direction of the inclined surface will be the sine component acting downwards.

The above two forces balance each other. Hence, the net force on the block will be zero. Hence, the forces acting can be mathematically expressed as,
$mg\sin 30{}^\circ -T=0$
Substituting the given values, we get
$ T=2\times 9.8\times \dfrac{1}{2}$
$\therefore T=9.8N$

Hence, the reading of the spring balance $9.8\;N$.

Note: The tension across a completely stretched rope is the same at every point, and the spring gets stretched even when the direction of force is opposite on its both ends, that’s why we added up all the forces on the spring, instead of cancelling them. We have used Newton’s second law in this question, which states that total force applied on an object is directly proportional to the rate of change of momentum. Mathematically, $F=ma$.