Question

What is the radius of the incircle of the right-angle triangle whose sides measures are 6, 8 and 10 units?
A. 1 unit
B. 2 units
C. 3 units
D. 4 units

Answer 1

Hint: We first explain the term of incircle, incentre and inradius. Then we draw the whole diagram and assume the inradius. We use the formula of the area of the right-angle triangle to form the equation for the $\Delta ABC=\Delta OAB+\Delta OBC+\Delta OAC$ Solving for the variable we find the solution.

Complete step by step answer:
We first explain the terms incircle, incentre and inradius. The intersecting point of all the angle bisectors of a triangle is called the incentre of that triangle. Then we take the perpendicular distance from the incentre to any one of the sides of the triangle and draw a circle with that value which becomes the incircle of the triangle. The radius of the circle is called the inradius of the triangle.

We now draw the right-angle triangle whose sides measure 6, 8 and 10 units. Then we draw its incircle. $\Delta ABC$ is the triangle, O is the incentre and the inradii are $OD=OE=OF$.

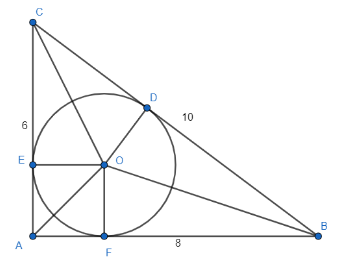
We know the area of a right-angle triangle is half of the multiplication of the sides containing the right angle. Also, for an area of $\Delta ABC$, we can write $\Delta ABC=\Delta OAB+\Delta OBC+\Delta OAC$.
We assume the inradii to be $OD=OE=OF=r$. We also have $AB=8,BC=10,AC=6$.
Forming the equation for $\Delta ABC=\Delta OAB+\Delta OBC+\Delta OAC$, we get
$\dfrac{1}{2}\times AC\times AB=\dfrac{1}{2}\times OF\times AB+\dfrac{1}{2}\times OD\times BC+\dfrac{1}{2}\times OE\times AC$.

Putting the values and simplifying we get
$\dfrac{1}{2}\times 6\times 8=\dfrac{1}{2}\times r\times 8+\dfrac{1}{2}\times r\times 10+\dfrac{1}{2}\times r\times 6$.
$\Rightarrow \dfrac{1}{2}\times 6\times 8=\dfrac{1}{2}\times r\times 8+\dfrac{1}{2}\times r\times 10+\dfrac{1}{2}\times r\times 6 \\
\Rightarrow 48=8r+10r+6r=24r \\
\therefore r=\dfrac{48}{24}=2 $
Therefore, the inradius of the triangle is 2units.

Hence, the correct option is B.

Note: The inradius can be found for any side as they will be similar for the incircle. The short formula to find the inradius for a right-angle triangle whose sides measures are $a,b,c$ will be equal to $r=\dfrac{ab}{a+b+c}$ where it is given that the hypotenuse is of length $c$.