Question

Prove the identity, $ \sin (A + \pi ) = - \sin A $

Answer 1

Hint: Imagine a unit circle and assume an angle, θ. Mark the corresponding coordinates $ (\cos \theta ,\sin \theta ) $ on the circle. The angle in the question is π more than the unknown angle. In the circle the coordinates corresponding to $ (\pi + \theta ) $ is $ ( - \cos \theta , - \sin \theta ) $ . Thus, we see the sine function for θ has changed to negative sine function upon addition of π.

Complete step-by-step answer:
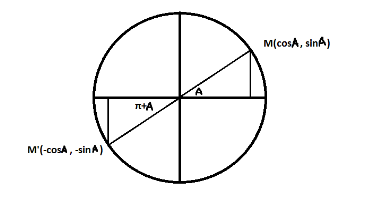
Let us visualize a circle with unit radius and center at origin. Then we mark the angle A on the positive $ (x,y) $ axis. The corresponding point on the circle “M” is $ (\cos A,\sin A) $ . When the angle is changed to $ (\pi + A) $ , the point “M’” has the coordinates $ ( - \cos A, - \sin A) $ as they are located in the III quadrant, i.e., negative x and y axis.
And hence we see, $ \sin (A + \pi ) = - \sin A $ .

Alternate method: Using the identity of summation of angles in the sine function, we can also verify the above asked identity.
We know that, $ \sin (a + b) = \sin a.\cos b + \sin b.\cos a $
Putting $ a = \pi \& b = A $ in the above identity,
 $ \sin (\pi + A) = \sin \pi .\cos A + \sin A.\cos \pi \\
Since
\sin \pi = 0 and \cos \pi = -1
we have
 $ \sin (A + \pi ) = - \sin A $
Hence, verified.

Note: The functions sine, cosine and tangent of an angle are sometimes remarked as the primary or basic trigonometric functions. The remaining trigonometric functions secant (sec), cosecant (csc), and cotangent (cot) are defined as reciprocals of cosine, sine, and tangent, respectively. Trigonometric identities are equations involving the trigonometric functions that are true for each value of the variables involved.