Question

Prove that the tangents drawn at the end of a diameter of a circle are parallel.

Answer 1

Hint: If we assume the slope of diameter of a circle to be ‘m’ and use the result for perpendicular lines ${{m}_{1}}{{m}_{2}}=-1$ where ${{m}_{1}}$ and ${{m}_{2}}$ are slopes of two perpendicular lines. Then we can easily show that the tangents at the end of a diameter of a circle are parallel.

Complete step-by-step answer:

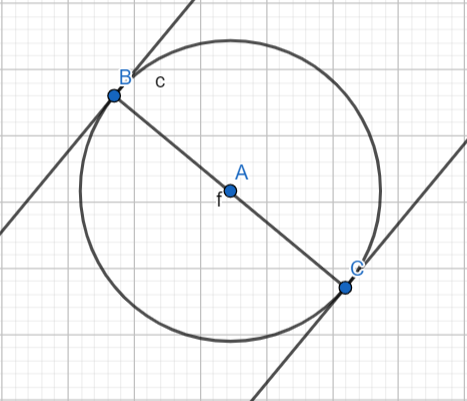
Let us assume the slope of the diameter, tangent-1 and tangent-2 to be $m$ , ${{m}_{1}}$ and ${{m}_{2}}$ . Now we know that tangents drawn at a point are perpendicular to diameter drawn at the same point. (Refer to the above figure). Therefore for tangent-1 we have, $m\cdot {{m}_{1}}=-1\Rightarrow {{m}_{1}}=\dfrac{-1}{m}$ …(i). Similarly for tangent-2 we have, $m\cdot {{m}_{2}}=-1\Rightarrow {{m}_{2}}=\dfrac{-1}{m}$ …(ii).
Comparing equation (i) and (ii) we have,
${{m}_{1}}={{m}_{2}}$
Therefore, the slope of both the lines are equal.
We should know that lines having the same slope are either parallel or coincident. Since, we know that the tangents are drawn at two different points so they cannot be coincident. Therefore, we can say that the tangents drawn at the ends of a diameter are parallel.
Hence, proved.
Note: The result ${{m}_{1}}{{m}_{2}}=-1$ is valid for any pair of perpendicular lines except lines parallel to x-axis and y-axis. Slope of the line parallel to the x-axis is equal to 0 and slope of line parallel to y-axis is not defined. Therefore their product is also not defined. But this is the only exception for this rule and applies to any pair of perpendicular lines in 2-D plane.