Question

Prove that the perimeter of a triangle is greater than the sum of the medians.

Answer 1

Hint: The median of a triangle is a line segment joining a vertex to the midpoint of the opposite side, and thus the side is bisected. We will compare the median with the respective sides of the triangle and try to show that the sum of all the three sides of the triangle is greater than the sum of all the medians of the triangle.

Complete step-by-step answer:
It is given in the question that we have to prove that the perimeter of a triangle is greater than the sum of its three medians. Basically, the median of a triangle is a line segment that joins a vertex to the midpoint of the opposite side, bisecting the side. It is to be noted that every triangle has three medians, one each from each vertex. Let us assume that PQR is a triangle in which PM, QN and RL are the medians of the triangle PQR as in the figure given below.

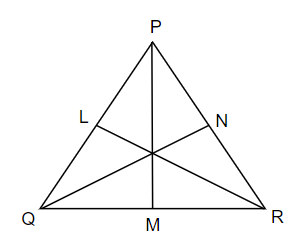
In the triangle PQR, we have PM, QN and RL as the three medians. If we compare the median PM with the side PQ, we come to know that PM < PQ as if we see in the right angle triangle PMQ, PQ is hypotenuse. Similarly, if we compare PM with PR, then we come to know that PM < PR. So, we get,
PM + PM < PQ + PR
2PM < PQ + PR ………… (i)
Similarly, if we compare RL with RP and RQ, then we get,
RL + RL < QR + RP
2RL < QR + RP ………… (ii)
Also, if we compare QN with QP and QR, then we get,
QN + QN < QP + QR
2QN < QP + QR ………… (iii)
On adding equations (i), (ii) and (iii), we get,
PQ + PR + QR + RP + QP + QR > 2PM + 2RL + 2QN
2(PQ + QR + RP) > 2 (PM + RL + QN)
Or, PQ + QR + RP > PM + RL + QN
We know that PQ + QR + RP is the perimeter of the triangle and PM + RL + QN is the sum of the median of the triangle PQR. Thus, the sum of the perimeter of the triangle is greater than the sum of all the medians of the triangle. Hence it is proved.

Note: Students must note that the altitude and median of a triangle are different, they must not get confused with the terms. Altitudes are perpendiculars dropped from the vertex to the opposite sides and medians are the lines dropped from the vertex to the midpoint of the opposite sides. Only in equilateral triangles, these are the same. Here, we have added the equations and also altered the inequality as per the terms in order to prove the desired result, so the operation to be performed on the equations at hand must be taken care of.