Question

Prove that the lengths of the tangents drawn from an external point to a circle are equal.

Answer 1

Hint: Here, we will use the property of tangents which states that any tangent drawn to the circle from an external point is perpendicular to the radius of the circle at the point of contact.
We will also use the property of right-angle triangle which states that for any right-angle triangle having Base, Perpendicular, and Hypotenuse:
\[{\left( {{\text{Hypotenuse}}} \right)^2} = {\left( {{\text{Perpendicular}}} \right)^2} + {\left( {{\text{Base}}} \right)^2}\]
This formula is also known as Pythagoras Theorem.

Complete step-by-step answer:
Step 1: We will construct two tangents to a circle with Centre at \[{\text{O}}\] from the external point \[{\text{T}}\] which touches the circle at a point \[{\text{P}}\] and \[{\text{Q}}\]:

Step 2: Now in figure (1) we will construct line segments by joining the points \[{\text{P}}\],\[{\text{Q}}\]and \[{\text{T}}\]with the Centre point \[{\text{O}}\] of the circle:

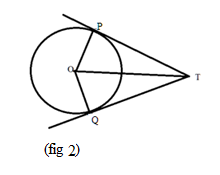
Now, from the figure (2) \[{\text{OP}}\] and \[{\text{OQ}}\] are the radii of the circle.
Step 3: We know that any tangent drawn to the circle from an external point is perpendicular to the radius of the circle at the point of contact.
Thus, in \[\Delta {\text{POT}}\] and \[\Delta {\text{QOT}}\], \[{\text{PT}}\] and \[{\text{QT}}\]are tangents and \[{\text{OP}}\],\[{\text{OQ}}\] are perpendicular to the tangents, so both the triangles \[\Delta {\text{POT}}\] and \[\Delta {\text{QOT}}\] are right-angle triangles.
\[ \Rightarrow \angle {\text{OPT = }}\angle {\text{OQT}} = {90^0}\]
Step 4: Now, in \[\Delta {\text{POT}}\], where the hypotenuse is equal to \[{\text{OT}}\], perpendicular is equal to \[{\text{OP}}\]and the base is equal to \[{\text{PT}}\], by applying Pythagoras theorem i.e. \[{\left( {{\text{Hypotenuse}}} \right)^2} = {\left( {{\text{Perpendicular}}} \right)^2} + {\left( {{\text{Base}}} \right)^2}\] in \[\Delta {\text{POT}}\], we get:
\[ \Rightarrow {\left( {{\text{OT}}} \right)^2} = {\left( {{\text{OP}}} \right)^2} + {\left( {{\text{PT}}} \right)^2}\]
Now, by bringing \[{\left( {{\text{PT}}} \right)^2}\]into the LHS side we get:
\[ \Rightarrow {\left( {{\text{OT}}} \right)^2} - {\left( {{\text{PT}}} \right)^2} = {\left( {{\text{OP}}} \right)^2}\]………………….…… (1)
Step 5: Similarly, in\[\Delta {\text{QOT}}\], where the hypotenuse is equal to \[{\text{OT}}\], perpendicular is equal to \[{\text{OQ}}\] and the base is equal to \[{\text{QT}}\], by applying Pythagoras theorem i.e. \[{\left( {{\text{Hypotenuse}}} \right)^2} = {\left( {{\text{Perpendicular}}} \right)^2} + {\left( {{\text{Base}}} \right)^2}\] in \[\Delta {\text{QOT}}\], we get:
\[ \Rightarrow {\left( {{\text{OT}}} \right)^2} = {\left( {{\text{OQ}}} \right)^2} + {\left( {{\text{QT}}} \right)^2}\]
By bringing, \[{\left( {{\text{QT}}} \right)^2}\] into the LHS side we get:
\[ \Rightarrow {\left( {{\text{OT}}} \right)^2} - {\left( {{\text{QT}}} \right)^2} = {\left( {{\text{OQ}}} \right)^2}\] ………………………. (2)
We know that,\[{\text{OP}}\] and \[{\text{OQ}}\] are the radius of the circle so both are equal.
\[ \Rightarrow {\text{OP}} = {\text{OQ}}\]
By substituting \[{\text{OQ = OP}}\]this value in the above equation (2):
\[ \Rightarrow {\left( {{\text{OT}}} \right)^2} - {\left( {{\text{QT}}} \right)^2} = {\left( {{\text{OP}}} \right)^2}\] ……………. (3)
Step 6: Thus, by comparing equations (1) and (3), we see that the RHS side of both the equations are equal so we can write:
\[ \Rightarrow {\left( {{\text{OT}}} \right)^2} - {\left( {{\text{PT}}} \right)^2} = {\left( {{\text{OT}}} \right)^2} - {\left( {{\text{QT}}} \right)^2}\] (\[\because \] RHS of (1) and (3) are same)
By subtracting \[{\left( {{\text{OT}}} \right)^2}\] from both LHS and RHS side, we get:
\[ \Rightarrow - {\left( {{\text{PT}}} \right)^2} = - {\left( {{\text{QT}}} \right)^2}\]
Now, in both LHS and RHS side negative sign and power are the same, so by simplifying the equation \[ - {\left( {{\text{PT}}} \right)^2} = - {\left( {{\text{QT}}} \right)^2}\] we get:
\[ \Rightarrow {\text{PT}} = {\text{QT}}\]
Hence, tangents of the circle \[{\text{PT}}\]and \[{\text{QT}}\] are equal.

Note: Students should remember the property of tangents that any tangents drawn to the circle at any point are perpendicular to the radius of the circle through the point of contact.
At the time of using Pythagoras theorem which is \[{\left( {{\text{Hypotenuse}}} \right)^2} = {\left( {{\text{Perpendicular}}} \right)^2} + {\left( {{\text{Base}}} \right)^2}\]in step numbers 4 and 5, you should take care of the symbols while bringing the terms RHS side to the LHS side or vice-versa.