Question

Prove that ${{\cot }^{2}}\dfrac{\pi }{6}+\csc \dfrac{5\pi }{6}+3{{\tan }^{2}}\dfrac{\pi }{6}=6$

Answer 1

Hint: Use the fact that $\cot \left( \dfrac{\pi }{6} \right)=\sqrt{3},\csc \left( \dfrac{\pi }{6} \right)=2$ and $\tan \left( \dfrac{\pi }{6} \right)=\dfrac{1}{\sqrt{3}}$.Use the fact that $\csc \left( \pi -x \right)=\csc x$. Substitute these values in the expression and simplify and hence prove L.H.S. = R.H.S.
Complete step-by-step answer:
Trigonometric ratios:
There are six trigonometric ratios defined on an angle of a right-angled triangle which are sine, cosine, tangent, cotangent, secant and cosecant.
The sine of an angle is defined as the ratio of the opposite side to the hypotenuse.
The cosine of an angle is defined as the ratio of the adjacent side to the hypotenuse.
The tangent of an angle is defined as the ratio of the opposite side to the adjacent side.
The cotangent of an angle is defined as the ratio of the adjacent side to the opposite side.
The secant of an angle is defined as the ratio of the hypotenuse to the adjacent side.
The cosecant of an angle is defined as the ratio of the hypotenuse to the opposite side.
Observe that sine and cosecant are multiplicative inverses of each other, cosine and secant are multiplicative inverses of each other, and tangent and cotangent are multiplicative inverses of each other.
We have the following table for the trigonometric ratios of $0,\dfrac{\pi }{6},\dfrac{\pi }{4},\dfrac{\pi }{3},\dfrac{\pi }{2}$

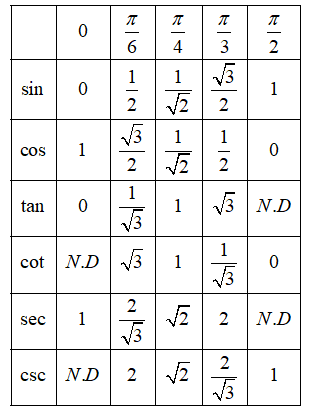
From the above table, we have
$\cot \left( \dfrac{\pi }{6} \right)=\sqrt{3},\csc \left( \dfrac{\pi }{6} \right)=2$ and $\tan \left( \dfrac{\pi }{6} \right)=\dfrac{1}{\sqrt{3}}$
Also, we have
$\csc \left( \dfrac{5\pi }{6} \right)=\csc \left( \pi -\dfrac{\pi }{6} \right)$
We know that $\csc \left( \pi -x \right)=\csc x$
Hence, we have
$\csc \left( \dfrac{5\pi }{6} \right)=\csc \left( \dfrac{\pi }{6} \right)=2$
Hence, we have
${{\cot }^{2}}\dfrac{\pi }{6}+\csc \dfrac{5\pi }{6}+3{{\tan }^{2}}\dfrac{\pi }{6}={{\left( \sqrt{3} \right)}^{2}}+2+3{{\left( \dfrac{1}{\sqrt{3}} \right)}^{2}}=3+2+1=6$
Hence, we have
L.H.S = R.H.S
Q.E.D
Note: [1] Rule for converting $T\left( n\dfrac{\pi }{2}\pm x \right)$ to $T\left( x \right)$, where T is any trigonometric ratio.
If n is even the final expression will be of T. If n is odd, the final expression will contain the complement of T.
The complement of sin is cos and vice versa
The complement of tan is cot and vice versa
The complement of cosec is sec and vice versa.
Sign of the final expression is determined by the quadrant in which $n\dfrac{\pi }{2}\pm x$ falls.
Keeping the above points in consideration, we have
$\csc \left( \pi -x \right)=\csc \left( 2\dfrac{\pi }{2}-x \right)$
Now 2 is even, hence the final expression will be of cosec x.
Also, $\pi -x$ falls in the second quadrant in which cosec x is positive
Hence, we have
$\csc \left( \pi -x \right)=\csc x$