Question

Prove that an exterior angle of cyclic quadrilateral is congruent to the angle opposite to its adjacent interior angle.

Answer 1

Hint:In this question first, we draw a figure in which a quadrilateral is inside a circle. We draw a straight line from one of the vertices of the quadrilateral and take a point on the corresponding line but the point should be exterior to the circle. We have to prove that “exterior angle of a cyclic quadrilateral is congruent to the angle opposite to its adjacent interior angle”.

Complete step by step answer:

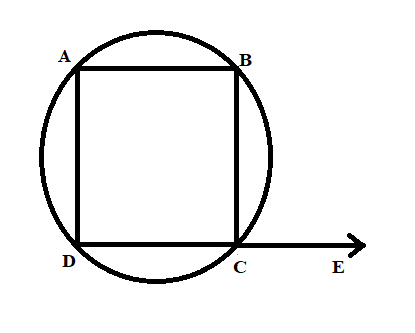
As per the problem statement, in the quadrilateral ABCD, side DC extends to the point E. Now, there is a straight-line DE in the figure.
We are required to prove that $\angle BCE$ and $\angle BAD$ are the congruent.
Proof: The angle BCD and the angle BCE forms a linear pair. So, the sum of both the angles are ${{180}^{\circ }}$ which is evident from the figure. Therefore, we form equation (1) as:
$\angle BCE+\angle BCD={{180}^{\circ }}...(1)$
Similarly, the sum of angle BAD and the angle BCD are ${{180}^{\circ }}$ by the property that the opposite angle of cyclic quadrilateral are ${{180}^{\circ }}$.
$\angle BAD+\angle BCD={{180}^{\circ }}...(2)$
We consider the above equation number as the equation (2).
Now, from equation (1) and equation (2), we concluded that the angle BCE and the angle BAD are the congruent. So, it can be mathematically expressed as,
$\angle BCE\simeq \angle BAD$
Hence, we proved that the “an exterior angle of cyclic quadrilateral is congruent to the angle opposite to its adjacent interior angle”.

Note: The keys for solving this problem is the knowledge of cyclic quadrilateral and associated properties. Students must draw the diagram of the problem statement for ease in writing of equations. This knowledge is very helpful in solving complex problems.